Solubility

From ChemPRIME and UCDavis Chemwiki

We have defined a solution as a homogeneous mixture of two more substances previously, that is, a mixture which appears to be uniform throughout. Under this definition we would refer to sugar or salt dissolved in water as solutions, but we would not apply the term to muddy water or to milk. A close inspection of muddy water reveals that it is not uniform in appearance but consists of small solid particles dispersed in water. We refer to such a mixture as a suspension. Under the microscope, milk can also be seen to be nonuniform, it consists of small drops of milk fat dispersed throughout an aqueous phase.

Our definition of a solution in terms of the homogeneity of a mixture is somewhat unsatisfactory since it does not tell us where to draw the line. Field-emission microscopes and electron microscopes have now been developed which can just about ”see” a single atom. With such a microscope virtually all matter looks nonuniform and hence not homogeneous. If our definition extends to such microscopes, then true solutions do not exist. In practice we draw the line somewhere around the 5 nanometer (nm) mark, even though some molecules are larger than this. 

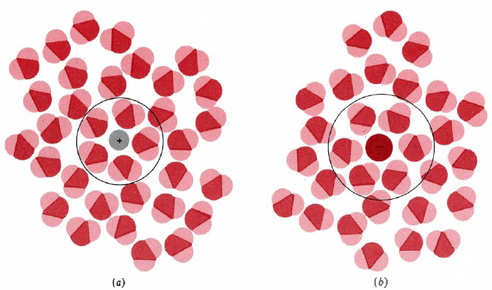
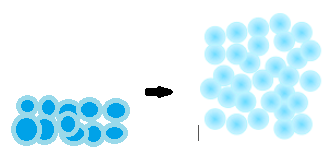
Figure 1

Suspensions and solutions viewed on the microscopic level. (a) A solution corresponds to a random arrangement of one kind of molecule around the other. (b) In a suspension there are small regions of space where only one kind of molecule exists.

On the molecular level a solution corresponds to the random arrangement of one kind of molecule or ion around another. In the accompanying figure, the illustration on the left corresponds to a solution since each black molecule is randomly surrounded by black and red molecules, and vice versa. The illustration on the right is a suspension. The distribution is not random, and most red molecules have red neighbors, while most black molecules have black neighbors.

Strictly speaking, the term solution applies to any homogeneous mixture, but we will concentrate our discussion on those solutions which involve liquids since these are the most common. It should be realized, though, that other types of solutions also exist. Air is a solution of a large number of gases (oxygen is the most concentrated) in another gas (nitrogen). A 5-cent coin is made from an alloy in which one solid (nickel) is dissolved in another (copper). Solutions of hydrogen gas in solid palladium and some other metals are also possible.

As mentioned in the brief discussion of solutions earlier, it is sometimes difficult to decide which component of a solution is the solute and which is the solvent. Usually the amount of solvent is much larger than that of the solute. If the pure components were initially in separate phases (a gas and a solid, for example), the phase corresponding to the state of the solution is taken to be the solvent. In the case of H₂(g) and Pd(s) mentioned above, for example, Pd would be the solvent because the solution is a solid phase.

Ionic Solutions

We have already stated several times that solubility in water is a characteristic property of many ionic compounds, and our discussion of Precipitation Reactions provides further confirmation of this fact. We have also presented experimental evidence that ions in solution are nearly independent of one another. This raises an important question, though, because we have also stated that attractive forces between oppositely charged ions in a crystal lattice are large. The high melting and boiling points of ionic compounds provide confirmation of the expected difficulty of separating oppositely charged ions. How, then, can ionic compounds dissolve at room temperature? Surely far more energy would be required for an ion to escape from the crystal lattice into solution than even the most energetic ions would possess. 

Figure 2

The hydration of (a) a positive ion; (b) a negative ion. When ions are dissolved in water, they attract and hold several water dipoles around them shown in the circular area in the circular area in the center of each part of the diagram.

The resolution of this apparent paradox lies in the interactions between ions and the molecules of water or other polar solvents. The negative (oxygen) side of a dipolar water molecule attracts and is attracted by any positive ion in solution. Because of this ion-dipole force, water molecules cluster around positive ions, as shown in Figure 2a. Similarly, the positive (hydrogen) ends of water molecules are attracted to negative ions. This process, in which either a positive or a negative ion attracts water molecules to its immediate vicinity, is called hydration (this process has been discussed briefly in other chapters of this text as well).

When water molecules move closer to ions under the influence of their mutual attraction, there is a net lowering of the potential energy of the microscopic particles. This counteracts the increase in potential energy which occurs when ions are separated from a crystal lattice against their attractions for other ions.

Thus the process of dissolving an ionic solid may be divided into the two hypothetical steps shown in Fig. 3. First, the crystalline salt is separated into gaseous ions. The heat energy absorbed when the ions are separated this way is called the lattice energy (or sometimes the lattice enthalpy). Next, the separate ions are placed in solution; that is, water molecules are permitted to surround the ions. The enthalpy change for this process is called the hydration enthalpy (or heat of hydration).

Figure 3

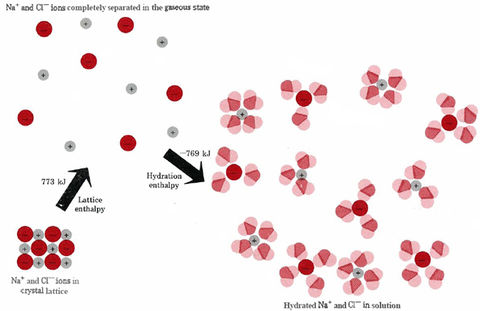
Enthalpy changes and solution. There is usually very little energy or enthalpy change when ionic solids like NaCl dissolve in H2O since the energy needed to separate the ions from each other is not very different from the energy liberated when the ions become hydrated by attracting H2O dipoles around them.

Since there is a lowering of the potential energy of the ions and water molecules, heat energy is given off and hydration enthalpies are invariably negative.

The heat energy absorbed when a solute dissolves (at a pressure of 1.00 atm) is called the enthalpy (or heat) of solution. It can be calculated using Hess' law, provided the lattice enthalpy and hydration enthalpy are known.

EXAMPLE 1 Using data given in Fig. 3, calculate the enthalpy of solution for NaCl(s). 

When NaCl(s) dissolves, 773 kJ is required to pull apart a mole of Na⁺ ions from a mole of Cl^– ions, but almost all of this requirement is provided by the 769 kJ released when the mole of Na⁺ and the mole of Cl^– becomes surrounded by water dipoles. Only 4 kJ of heat energy is absorbed from the surroundings when a mole of NaCl(s) dissolves. You can verify the small size of this enthalpy change by putting a few grains of salt on your moist tongue. The quantity of heat energy absorbed as the salt dissolves is so small that you will feel no cooling, even though your tongue is quite a sensitive indicator of temperature changes.

Few molecules are both small enough and polar to cluster around positive and negative ions in solution as water does. Consequently water is one of the few liquids which readily dissolves many ionic solids. Hydration of Na⁺, Cl^– and other ions in aqueous solution prevents them from attracting each other into a crystal lattice and precipitating. 

Non-ionic solutions

In general the stable form of a substance at any given temperature will always be that which leads to the best balance between low potential energy and high molecular disorder.To see how these considerations are applied to solutions, think about the individual steps that must be carried out when a solute is dissolved in a solvent:

1.  If the solute is a solid or liquid, it must first be dispersed — that is, its molecular units must be pulled apart. This requires energy, and so this step always works against solution formation. This process requires an absorption of energy. 2. Separating the solvent molecules from one another to "make room" for the solute particles also requires an absorption of energy.

endothermic                                                               endothermic

3.  Energy is released as the solvent particles and solvent molecules interact in the solution (exothermic). The overall dissolution process is exothermic if the amount of heat absorbed in steps 1 and 2 is less than the amount of energy released in step 3 (and is favored). The process is endothermic (and disfavored) if the amount of energy absorbed in steps 1 and 2 is greater than the amount of heat released in step 3.

exothermic Overall Process Exothermic if A-B attractions stronger than A-A + B-B. (favored) Endothermic if attractions between like molecules are stronger than those between unlike molecules. (disfavored)

 

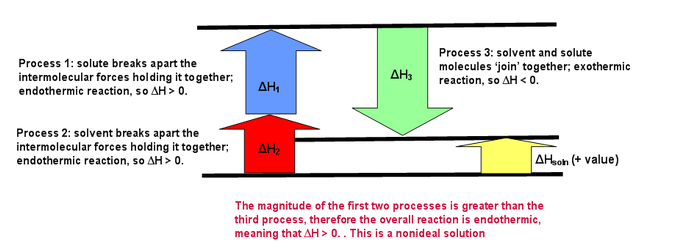
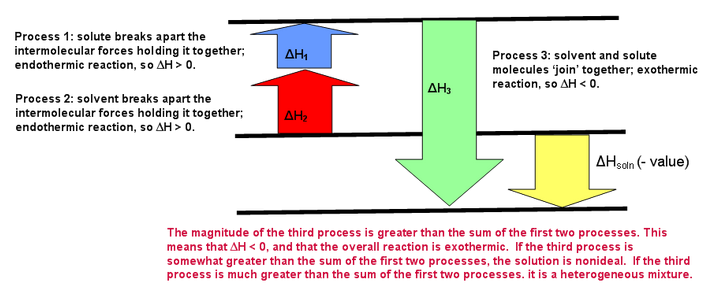
If step 3 releases more energy than is consumed in step 1 and 2, this will favor solution formation, and we can generally expect the solute to be soluble in the solvent. Even if the dissolution process is slightly endothermic, there is a third important factor, the entropy increase (increase in disorder), that will very often favor the dissolved state. The following figures illustrate exothermic and endothermic dissolving processes as well as an ideal dissolving process (where steps 1 and 2 = step 3). In these figures `DeltaH1=DeltaH_(solute)`      `DeltaH2= DeltaH_(solvent)` and `DeltaH3= ?DeltaH_(mixing)

Energy Diagram for Endothermic Dissolving Process (where `DeltaH_(solution)>0`)

Energy Diagram for Exothermic Dissolving Process (where `DeltaH_(solution) < 0`)

Energy Diagram for an Ideal Solution (`DeltaH<sub>_(solution)</sub> = 0`)

Example 2
Which process(es) is the simple formation of a solution, and which process(es) involves a chemical reaction?

1. mixing an aqueous solution of NaOH with an aqueous solution of Hal
2. bubbling Hal gas through water
3. adding iodine crystals to CCl₄
4. adding sodium metal to ethanol to produce sodium ethoxide (C₂H₅O Na⁺) and hydrogen gas

Example 3

Draw a generic energy diagram (you do not need exact values) of adding ammonium nitrate to water, which is the process contained in ice packs.