Vapor Pressure

Many of the physical properties of solutions differ significantly from those of the pure substances discussed in earlier chapters, and these differences have important consequences. For example, the limited temperature range of liquid water (0°C–100°C) severely limits its use. Aqueous solutions have both a lower freezing point and a higher boiling point than pure water. Probably one of the most familiar applications of this phenomenon is the addition of ethylene glycol (“antifreeze”) to the water in an automobile radiator. This solute lowers the freezing point of the water, preventing the engine from cracking in very cold weather from the expansion of pure water on freezing. Antifreeze also enables the cooling system to operate at temperatures greater than 100°C without generating enough pressure to explode.

Changes in the freezing point and boiling point of a solution depend primarily on the number of solute particles present rather than the kind of particles. Such properties of solutions are called colligative properties (from the Latin colligatus, meaning “bound together” as in a quantity). As we will see, the vapor pressure and osmotic pressure of solutions are also colligative properties.

When we determine the number of particles in a solution, it is important to remember that not all solutions with the same molarity contain the same concentration of solute particles. Consider, for example, 0.01 M aqueous solutions of sucrose, NaCl, and CaCl2. Because sucrose dissolves to give a solution of neutral molecules, the concentration of solute particles in a 0.01 M sucrose solution is 0.01 M. In contrast, both NaCl and CaCl2 are ionic compounds that dissociate in water to yield solvated ions. As a result, a 0.01 M aqueous solution of NaCl contains 0.01 M Na+ ions and 0.01 M Cl? ions, for a total particle concentration of 0.02 M. Similarly, the CaCl2 solution contains 0.01 M Ca2+ ions and 0.02 M Cl? ions, for a total particle concentration of 0.03 M.These values are correct for dilute solutions, where the dissociation of the compounds to form separately solvated ions is complete. At higher concentrations (typically >1 M), especially with salts of small, highly charged ions (such as Mg2+ or Al3+), or in solutions with less polar solvents, dissociation to give separate ions is often incomplete. The sum of the concentrations of the dissolved solute particles dictates the physical properties of a solution. In the following discussion, we must therefore keep the chemical nature of the solute firmly in mind.

Vapor Pressure of Solutions and Raoult’s Law

Vapor pressure depends on the escaping tendency of solvent molecules from the liquid phase. You will recall that the vapor pressure is a direct measure of escaping tendency, so we can use these terms more or less interchangeably.

The tendency of molecules to escape from a liquid phase into the gas phase depends in part on how much of an increase in entropy can be achieved in doing so. Evaporation of solvent molecules from the liquid always leads to a large increase in entropy because of the greater volume occupied by the molecules in the gaseous state. But if the liquid solvent is initially “diluted“ with solute, its entropy is already larger to start with, so the amount by which it can increase on entering the gas phase will be less. There will accordingly be less tendency for the solvent molecules to enter the gas phase, and so the vapor pressure of the solution diminishes as the concentration of solute increases and that of solvent decreases.

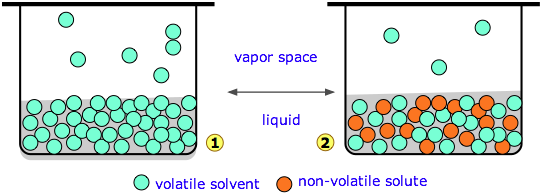
Diagram 1 (above left) represents pure water whose concentration in the liquid is 55.5 M. A tiny fraction of the H₂O molecules will escape into the vapor space, and if the top of the container is closed, the pressure of water vapor builds up until equilibrium is achieved. Once this happens, water molecules continue to pass between the liquid and vapor in both directions, but at equal rates, so the partial pressure of H₂O in the vapor remains constant at a value known as the vapor pressure of water at the particular temperature.

In the system below, we have replaced a fraction of the water molecules with a substance that has zero or negligible vapor pressure — a nonvolatile solute such as salt or sugar. This has the effect of diluting the water, reducing its escaping tendency and thus its vapor pressure.

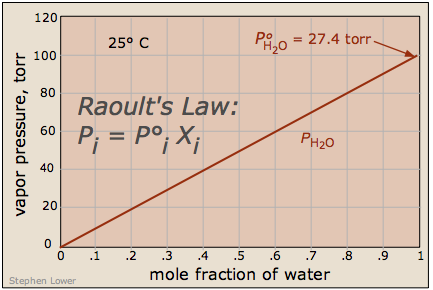
What's important to remember is that the reduction in the vapor pressure of a solution of this kind is directly proportional to the fraction of the [volatile] solute molecules in the liquid — that is, to the mole fraction of the solvent. The reduced vapor pressure is given by Raoult's law(1886):

Equation (1)
Where `P_A` is the vapor pressure of the solvent in solution, `chi_A` is the mole fraction of the solvent in solution, and `P_A^0` is the vapor pressure of the pure solvent. From the definition of mole fraction, you should understand that in a two-component solution (i.e., a solvent and a single solute), `chi_(solvent) = 1-chi_(solution)`

Example 6
Estimate the vapor pressure of a 40 percent (W/W) solution of ordinary cane sugar (C₂₂O₁₁H₂₂, 342 g mol^–1) in water. The vapor pressure of pure water at this particular temperature is 26.0 torr.

Solution:

100 g of solution contains (40g) `-:` (342 g `mol^(-1)`) = 0.12 mol of sugar and (60 g) `-:` (18 g `mol^(-1)`) = 3.3 mol of water. The mole fraction of water in the solution is

`(3.3)/(3.3 + 12) = 0.96`

and its vapor pressure will be 0.96 x 26.0 torr = 25.1 torr.  

Example 7
The vapor pressure of water at 10° C is 9.2 torr. Estimate the vapor pressure at this temperature of a solution prepared by dissolving 1 mole of CaCl₂ in 1 L of water.

Solution: 

Eacg mole of `CaCl_2` dissociates into one mole of `Ca^(2+)` and two moles of `Cl^(1-)`, giving a total of three moles of solute particles. The mole fraction of water in the solution will be:

`(55.5)/(3+55.5) = 0.95`

The vapor pressure will be 0.95 × 9.2 torr = 8.7 torr.

If the solution contains only a single nonvolatile solute (B), than the mole fraction of the solvent (`chi_A`) and the mole fraction of the solute (`chi_B`) when added together, will equal 1.
`chi_A+chi_B = 1`     (2)

We can substitute `chi_A = 1 - chi_B` to obtain the following equation
`P_A = (1-chi_b)P_A^0`   

`=P_A^0-chi_bP_A^0`   (4)

Rearranging and defining `DeltaP_A = P_A^0-P_A`, we obtain a relationship between the decrease in vapor pressure and the mole fraction of nonvolatile solute:

`P_A-P_A^0=DeltaP_A<sub>`</sub>

`=X_BP_A^0`   (5)

We can solve vapor pressure problems in either of two ways: by using equation 1 to calculate the actual vapor pressure above a solution of a nonvolatile solute, or by using equation 5 to calculate the decrease in vapor pressure caused by a specified amount of a nonvolatile solute.

Example 8 Ethylene glycol (HOCH₂CH₂OH), the major ingredient in commercial automotive antifreeze, increases the boiling point of radiator fluid by lowering its vapor pressure. At 100°C, the vapor pressure of pure water is 760 mmHg. Calculate the vapor pressure of an aqueous solution containing 30.2% ethylene glycol by mass, a concentration commonly used in climates that do not get extremely cold in winter.