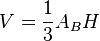Processing...

The cone calculator contains equations related to objects 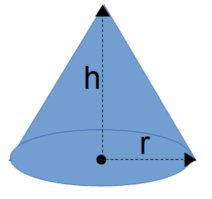/attachments/fa62cba3-0854-11e4-b7aa-bc764e2038f2/cone.jpg Right Perpendicular Cone Cone Frustum 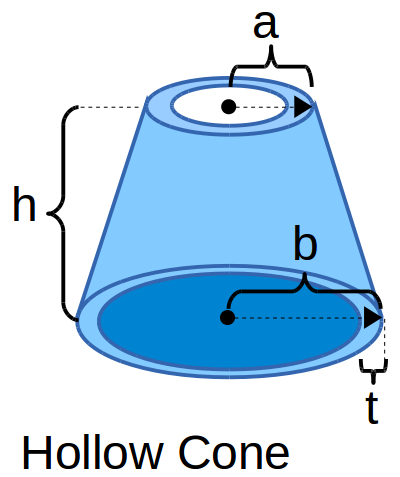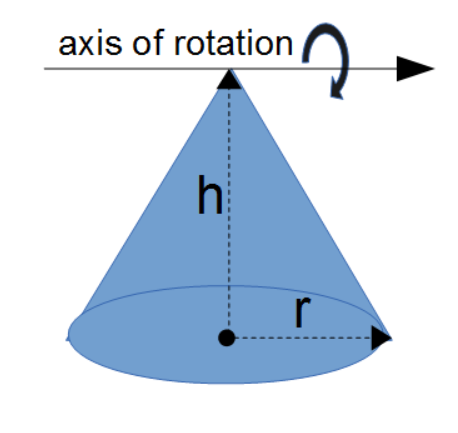Moments of Inertia
about different axes shaped like a right geometric circular cone including equations for volume, surface area, mass and moments of inertia.

Cone Calculator: The calculator functions for cones include the following:

Surface Area: cone surface area based on cone height and cone base radius
Volume: cone volume based on cone height and cone base radius
Mass: cone mass or weight as a function of the volume and mean density
Frustum Surface Area: cone frustum surface area based on the two heights and two radii
Frustum Volume: cone frustum volume based on the two heights and two radii
Frustum Mass: cone frustum weight or mass based on the cone frustum volume and mean density
Shell Volume: cone shell volume a.k.a. hollow cone volume
Shell Mass: cone shell mass or weight a.k.a. hollow cone mass
Moment of inertia of a cone shaped object based on mass and rotation axis
Moment of inertia of a cone shaped object based on mass and distance to apex (rotation around apex)

Mean Density, Mass and Moments of Inertia

For the mass equations, one can use the common mean densities formula to look up the mean density of common substances and then use the resulting value as input to the mass equation. The Mean Density Table Lookup button provides the mean density of hundreds (650+) of substances from gases, to metals, woods, foods, liquids and much more. The result are given in `"kg"/m^3` which is the default input units for the mass calculation.

The result of the mass equation can then be used in the equations for the moments of inertia.

Cone

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex.

More precisely, it is the solid figure bounded by a base in a plane and by a surface (called the lateral surface) formed by the locus of all straight line segments joining the apex to the perimeter of the base. The term "cone" sometimes refers just to the surface of this solid figure, or just to the lateral surface.

The axis of a cone is the straight line (if any), passing through the apex, about which the base (and the whole cone) has a rotational symmetry.

In common usage in elementary geometry, cones are assumed to be right circular, where circular means that the base is a circle and right means that the axis passes through the center of the base at right angles to its plane. Contrasted with right cones are oblique cones, in which the axis does not pass perpendicularly through the center of the base. In general, however, the base may be any shape and the apex may lie anywhere (though it is usually assumed that the base is bounded and therefore has finite area, and that the apex lies outside the plane of the base).

A cone with a polygonal base is called a pyramid.

Other Mathematical Meanings

In mathematical usage, the word "cone" is used also for an "infinite cone", the union of a set of half-lines that start at a common apex point and go through a base. An infinite cone is not bounded by its base but extends to infinity. A "doubly infinite cone", or "double cone", is the union of a set of straight lines that pass through a common apex point and go through a base, therefore double infinite cones extend symmetrically on both sides of the apex.

The boundary of an infinite or doubly infinite cone is a conical surface, and the intersection of a plane with this surface is a conic section. For infinite cones, the word axis again usually refers to the axis of rotational symmetry (if any). Either half of a double cone on one side of the apex is called a "nappe".

Depending on the context, "cone" may also mean specifically a convex cone or a projective cone.

Geometry

Surface area

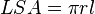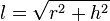The lateral surface area of a right circular cone is $LSA = \pi r l$ where r is the radius of the circle at the bottom of the cone and is the lateral height of the cone (given by the Pythagorean theorem $l=\sqrt{r^2+h^2}$ where 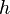is the height of the cone). The surface area of the bottom circle of a cone is the same as for any circle, $\pi r^2$ . Thus the total surface area of a right circular cone is:

$SA=\pi r^2+\pi r l$ or

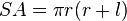
$SA=\pi r(r+l)$

Volume

The volume 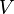of any conic solid is one third of the product of the area of the base 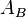A_B and the height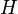

$V = \frac{1}{3}A_B H$

In modern mathematics, this formula can easily be computed using calculus – it is, up to scaling, the integral 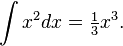$\int x^2 dx = \tfrac{1}{3} x^3.$ Without using calculus, the formula can be proven by comparing the cone to a pyramid and applying Cavalieri's principle – specifically, comparing the cone to a (vertically scaled) right square pyramid, which forms one third of a cube. This formula cannot be proven without using such infinitesimal arguments – unlike the 2-dimensional formulae for polyhedral area, though similar to the area of the circle – and hence admitted less rigorous proofs before the advent of calculus, with the ancient Greeks using the method of exhaustion. This is essentially the content of Hilbert's third problem – more precisely, not all polyhedral pyramids are scissors congruent (can be cut apart into finite pieces and rearranged into the other), and thus volume cannot be computed purely by using a decomposition argument.

Center of mass

The center of mass of a conic solid of uniform density lies one-quarter of the way from the center of the base to the vertex, on the straight line joining the two.

References

Wikipedia - http://en.wikipedia.org/wiki/Cone