13.8 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
work — the amount of energy transferred into or out of a system, excluding energy transferred by heat conduction
Notation
`W` — work
Summary
Work is a measure of the transfer of mechanical energy, i.e., the transfer of energy by a force rather than by heat conduction. When the force is constant, work can usually be calculated as
`W=F_?*|d|` ,[only if the force is constant]
where `d` is simply a less cumbersome notation for `Deltar`, the vector from the initial position to the final position. Thus,
- A force in the same direction as the motion does positive work, i.e., transfers energy into the object on which it acts.
- A force in the opposite direction compared to the motion does negative work, i.e., transfers energy out of the object on which it acts.
- When there is no motion, no mechanical work is done. The human body burns calories when it exerts a force without moving, but this is an internal energy transfer of energy within the body, and thus does not fall within the scientific definition of work.
- A force perpendicular to the motion does no work.
When the force is not constant, the above equation should be generalized as the area under the graph of `F_(?)` versus `d`.
Machines such as pulleys, levers, and gears may increase or decrease a force, but they can never increase or decrease the amount of work done. That would violate conservation of energy unless the machine had some source of stored energy or some way to accept and store up energy.
There are some situations in which the equation `W=F_(?)|d|` is ambiguous or not true, and these issues are discussed rigorously in section 13.6. However, problems can usually be avoided by analyzing the types of energy being transferred before plunging into the math. In any case there is no substitute for a physical understanding of the processes involved.
The techniques developed for calculating work can also be applied to the calculation of potential energy. We fix some position as a reference position, and calculate the potential energy for some other position, `x`, as
`PE_x=-W_("ref"->x.)`
The following two equations for potential energy have broader significance than might be suspected based on the limited situations in which they were derived:
`PE=1/2k(x-x_o)^2.`
[potential energy of a spring having spring constant `k`, when stretched or compressed from the equilibrium position `x_o`; analogous equations apply for the twisting, bending, compression, or stretching of any object.]
[gravitational potential energy of objects of masses `M` and `m`, separated by a distance `r`; an analogous equation applies to the electrical potential energy of an electron in an atom.]
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. Two speedboats are identical, but one has more people aboard than the other. Although the total masses of the two boats are unequal, suppose that they happen to have the same kinetic energy. In a boat, as in a car, it's important to be able to stop in time to avoid hitting things. (a) If the frictional force from the water is the same in both cases, how will the boats' stopping distances compare? Explain. (b) Compare the times required for the boats to stop.
2. In each of the following situations, is the work being done positive, negative, or zero? (a) a bull paws the ground; (b) a fishing boat pulls a net through the water behind it; (c) the water resists the motion of the net through it; (d) you stand behind a pickup truck and lower a bale of hay from the truck's bed to the ground. Explain. [Based on a problem by Serway and Faughn.]
3. In the earth's atmosphere, the molecules are constantly moving around. Because temperature is a measure of kinetic energy per molecule, the average kinetic energy of each type of molecule is the same, e.g., the average `KE` of the `O_2` molecules is the same as the average `KE` of the `N_2` molecules. (a) If the mass of an `O_2` molecule is eight times greater than that of a He atom, what is the ratio of their average speeds? Which way is the ratio, i.e., which is typically moving faster? (b) Use your result from part a to explain why any helium occurring naturally in the atmosphere has long since escaped into outer space, never to return. (Helium is obtained commercially by extracting it from rocks.) You may want to do problem 21 first, for insight.
4. Weiping lifts a rock with a weight of 1.0 N through a height of 1.0 m, and then lowers it back down to the starting point. Bubba pushes a table 1.0 m across the floor at constant speed, requiring a force of 1.0 N, and then pushes it back to where it started. (a) Compare the total work done by Weiping and Bubba. (b) Check that your answers to part a make sense, using the definition of work: work is the transfer of energy. In your answer, you'll need to discuss what specific type of energy is involved in each case.
5. In one of his more flamboyant moments, Galileo wrote “Who does not know that a horse falling from a height of three or four cubits will break his bones, while a dog falling from the same height or a cat from a height of eight or ten cubits will suffer no injury? Equally harmless would be the fall of a grasshopper from a tower or the fall of an ant from the distance of the moon.” Find the speed of an ant that falls to earth from the distance of the moon at the moment when it is about to enter the atmosphere. Assume it is released from a point that is not actually near the moon, so the moon's gravity is negligible. You will need the result of example 7 on p. 338. `sqrt`
6. [Problem 6 has been deleted.]
7. (a) The crew of an 18th century warship is raising the anchor. The anchor has a mass of 5000 kg. The water is 30 m deep. The chain to which the anchor is attached has a mass per unit length of 150 kg/m. Before they start raising the anchor, what is the total weight of the anchor plus the portion of the chain hanging out of the ship? (Assume that the buoyancy of the anchor is negligible.)
(b) After they have raised the anchor by 1 m, what is the weight they are raising?
(c) Define `y=0` when the anchor is resting on the bottom, and `y=+30` m when it has been raised up to the ship. Draw a graph of the force the crew has to exert to raise the anchor and chain, as a function of `y`. (Assume that they are raising it slowly, so water resistance is negligible.) It will not be a constant! Now find the area under the graph, and determine the work done by the crew in raising the anchor, in joules.
(d) Convert your answer from (c) into units of kcal. `sqrt`
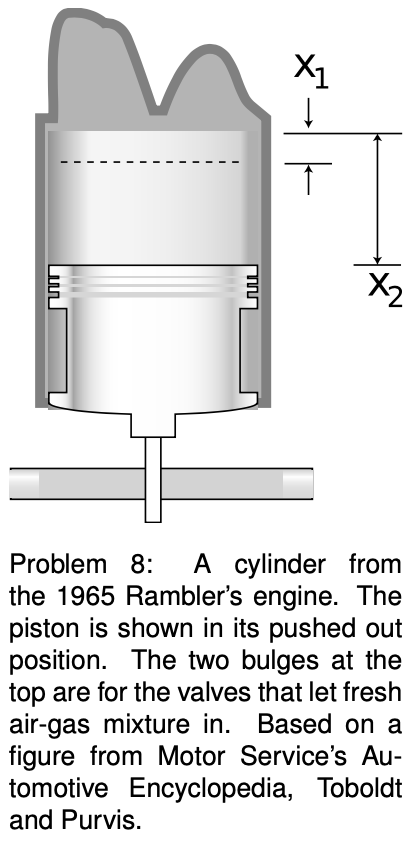8. In the power stroke of a car's gasoline engine, the fuel-air mixture is ignited by the spark plug, explodes, and pushes the piston out. The exploding mixture's force on the piston head is greatest at the beginning of the explosion, and decreases as the mixture expands. It can be approximated by `F=a"/"x`, where `x` is the distance from the cylinder to the piston head, and `a` is a constant with units of `N*m`. (Actually `a"/"x^(1.4)` would be more accurate, but the problem works out more nicely with `a"/"x!`) The piston begins its stroke at `x=x_1`, and ends at `x=x_2`. The 1965 Rambler had six cylinders, each with `a=220 N*m `, `x_1=1.2 cm`, and `x_2=10.2 cm`.
(a) Draw a neat, accurate graph of `F` vs `x`, on graph paper.
(b) From the area under the curve, derive the amount of work done in one stroke by one cylinder. `sqrt`
(c) Assume the engine is running at 4800 r.p.m., so that during one minute, each of the six cylinders performs 2400 power strokes. (Power strokes only happen every other revolution.) Find the engine's power, in units of horsepower (1 hp=746 W). `sqrt`
(d) The compression ratio of an engine is defined as `x_2"/"x_1`. Explain in words why the car's power would be exactly the same if `x_1` and `x_2` were, say, halved or tripled, maintaining the same compression ratio of 8.5. Explain why this would not quite be true with the more realistic force equation `F=a"/"x^1.4`.
9. The magnitude of the force between two magnets separated by a distance rr can be approximated as `kr^(-3)` for large values of `r`. The constant `k` depends on the strengths of the magnets and the relative orientations of their north and south poles. Two magnets are released on a slippery surface at an initial distance `r_i`, and begin sliding towards each other. What will be the total kinetic energy of the two magnets when they reach a final distance `r_f`?(Ignore friction.) `sqrt` `int`
10. A car starts from rest at `t=0`, and starts speeding up with constant acceleration. (a) Find the car's kinetic energy in terms of its mass, `m`, acceleration, `a`, and the time, `t`. (b) Your answer in the previous part also equals the amount of work, `W`, done from `t=0` until time `t`. Take the derivative of the previous expression to find the power expended by the car at time `t`. (c) Suppose two cars with the same mass both start from rest at the same time, but one has twice as much acceleration as the other. At any moment, how many times more power is being dissipated by the more quickly accelerating car? (The answer is not 2.) `sqrt` `int`
11. A space probe of mass `m` is dropped into a previously unexplored spherical cloud of gas and dust, and accelerates toward the center of the cloud under the influence of the cloud's gravity. Measurements of its velocity allow its potential energy, `PE`, to be determined as a function of the distance `r` from the cloud's center. The mass in the cloud is distributed in a spherically symmetric way, so its density, `rho(r)`, depends only on `r` and not on the angular coordinates. Show that by finding `PE`, one can infer `rho(r)` as follows:
`rho(r)=1/(4piGmr^2)d/(dr)(r^2(dPE)/(dr))`. `int` `***`
12. A rail gun is a device like a train on a track, with the train propelled by a powerful electrical pulse. Very high speeds have been demonstrated in test models, and rail guns have been proposed as an alternative to rockets for sending into outer space any object that would be strong enough to survive the extreme accelerations. Suppose that the rail gun capsule is launched straight up, and that the force of air friction acting on it is given by `F=be^(-cx)`, where `x` is the altitude, `b` and `c` are constants, and `e` is the base of natural logarithms. The exponential decay occurs because the atmosphere gets thinner with increasing altitude. (In reality, the force would probably drop off even faster than an exponential, because the capsule would be slowing down somewhat.) Find the amount of kinetic energy lost by the capsule due to air friction between when it is launched and when it is completely beyond the atmosphere. (Gravity is negligible, since the air friction force is much greater than the gravitational force.) `sqrt` `int`
13. A certain binary star system consists of two stars with masses `m_1`and `m_2`, separated by a distance `b`. A comet, originally nearly at rest in deep space, drops into the system and at a certain point in time arrives at the midpoint between the two stars. For that moment in time, find its velocity, `v`, symbolically in terms of `b`, `m_1`, `m_2`, and fundamental constants. `sqrt`
14. An airplane flies in the positive direction along the `x` axis, through crosswinds that exert a force `F=(a+bx)hatx +(c+dx)haty`. Find the work done by the wind on the plane, and by the plane on the wind, in traveling from the origin to position `x`. `int`
15. In 1935, Yukawa proposed an early theory of the force that held the neutrons and protons together in the nucleus. His equation for the potential energy of two such particles, at a center-to-center distance `r` was `PE(r)=gr^(-1)e^(-r/a)`, where `g` parametrizes the strength of the interaction, `e` is the base of natural logarithms, and `a` is about `10^(-15) m`. Find the force between two nucleons that would be consistent with this equation for the potential energy. `sqrt` `int`
16. Prove that the dot product defined in section 13.7 is rotationally invariant in the sense of section 7.5.
17. Fill in the details of the proof of `A*B=A_xB_x+A_yB_y+A_zB_z` on page 342.
18. Does it make sense to say that work is conserved?
19. (a) Suppose work is done in one-dimensional motion. What happens to the work if you reverse the direction of the positive coordinate axis? Base your answer directly on the definition of work. (b) Now answer the question based on the `W=Fd` rule.
20. A microwave oven works by twisting molecules one way and then the other, counterclockwise and then clockwise about their own centers, millions of times a second. If you put an ice cube or a stick of butter in a microwave, you'll observe that the solid doesn't heat very quickly, although eventually melting begins in one small spot. Once this spot forms, it grows rapidly, while the rest of the solid remains solid; it appears that a microwave oven heats a liquid much more rapidly than a solid. Explain why this should happen, based on the atomic-level description of heat, solids, and liquids. (See, e.g., figure b on page 311.)
Don't repeat the following common mistakes:
In a solid, the atoms are packed more tightly and have less space between them. Not true. Ice floats because it's less dense than water.
In a liquid, the atoms are moving much faster. No, the difference in average speed between ice at `-1°C` and water at `1°C` is only `0.4%`.
21. Starting at a distance `r` from a planet of mass `M`, how fast must an object be moving in order to have a hyperbolic orbit, i.e., one that never comes back to the planet? This velocity is called the escape velocity. Interpreting the result, does it matter in what direction the velocity is? Does it matter what mass the object has? Does the object escape because it is moving too fast for gravity to act on it? `sqrt`
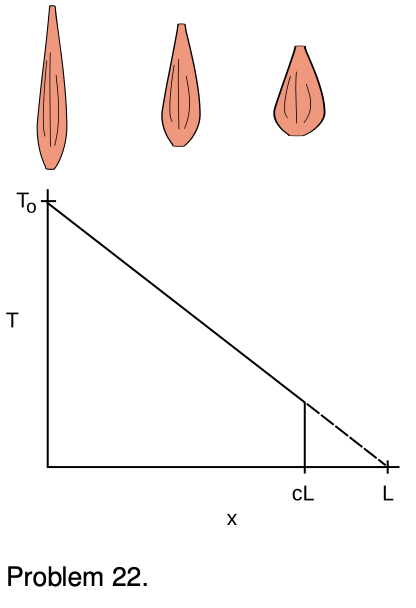22. The figure, redrawn from Gray's Anatomy, shows the tension of which a muscle is capable. The variable `x` is defined as the contraction of the muscle from its maximum length `L`, so that at `x=0` the muscle has length `L`, and at `x=L` the muscle would theoretically have zero length. In reality, the muscle can only contract to `x=cL`, where `c` is less than 1. When the muscle is extended to its maximum length, at `x=0`, it is capable of the greatest tension, `T_o`. As the muscle contracts, however, it becomes weaker. Gray suggests approximating this function as a linear decrease, which would theoretically extrapolate to zero at `x=L`.
(a) Find the maximum work the muscle can do in one contraction, in terms of `c`, `L`, and `T_o`. `sqrt`
(b) Show that your answer to part a has the right units.
(c) Show that your answer to part a has the right behavior when `c=0` and when `c=1`.
(d) Gray also states that the absolute maximum tension `T_o` has been found to be approximately proportional to the muscle's cross-sectional area `A` (which is presumably measured at `x=0`), with proportionality constant `k`. Approximating the muscle as a cylinder, show that your answer from part a can be reexpressed in terms of the volume, `V`, eliminating `L` and `A`. `sqrt`
(e) Evaluate your result numerically for a biceps muscle with a volume of `200 "cm"^3`, with `c=0.8` and `k=100 "N/cm"^2` as estimated by Gray. `sqrt`
23. A car accelerates from rest. At low speeds, its acceleration is limited by static friction, so that if we press too hard on the gas, we will “burn rubber” (or, for many newer cars, a computerized traction-control system will override the gas pedal). At higher speeds, the limit on acceleration comes from the power of the engine, which puts a limit on how fast kinetic energy can be developed.
(a) Show that if a force `F` is applied to an object moving at speed `v`, the power required is given by `P=vF`.
(b) Find the speed `v` at which we cross over from the first regime described above to the second. At speeds higher than this, the engine does not have enough power to burn rubber. Express your result in terms of the car's power `P`, its mass `m`, the coefficient of static friction `mu_s`, and `g`.
(c) Show that your answer to part b has units that make sense.
(d) Show that the dependence of your answer on each of the four variables makes sense physically.
(e) The 2010 Maserati Gran Turismo Convertible has a maximum power of `3.23×10^5` W (433 horsepower) and a mass (including a 50-kg driver) of `2.03×10^3 kg`. (This power is the maximum the engine can supply at its optimum frequency of `7600` r.p.m. Presumably the automatic transmission is designed so a gear is available in which the engine will be running at very nearly this frequency when the car is moving at `v`.) Rubber on asphalt has `mu_sapprox0.9`. Find `v` for this car. Answer: `18 m"/"s`, or about `40` miles per hour.
(f) Our analysis has neglected air friction, which can probably be approximated as a force proportional to `v^2`. The existence of this force is the reason that the car has a maximum speed, which is `176` miles per hour. To get a feeling for how good an approximation it is to ignore air friction, find what fraction of the engine's maximum power is being used to overcome air resistance when the car is moving at the speed `v` found in part e. Answer: `1%`
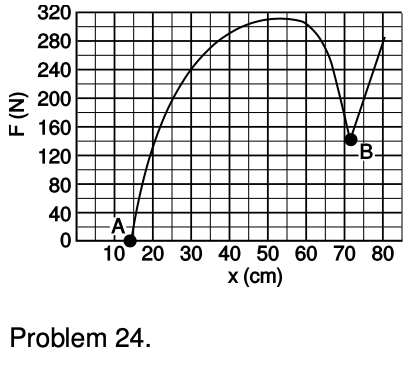24. Most modern bow hunters in the U.S. use a fancy mechanical bow called a compound bow, which looks nothing like what most people imagine when they think of a bow and arrow. It has a system of pulleys designed to produce the force curve shown in the figure, where `F` is the force required to pull the string back, and `x` is the distance between the string and the center of the bow's body. It is not a linear Hooke's-law graph, as it would be for an old-fashioned bow. The big advantage of the design is that relatively little force is required to hold the bow stretched to point `B` on the graph. This is the force required from the hunter in order to hold the bow ready while waiting for a shot. Since it may be necessary to wait a long time, this force can't be too big. An old-fashioned bow, designed to require the same amount of force when fully drawn, would shoot arrows at much lower speeds, since its graph would be a straight line from `A` to` B`. For the graph shown in the figure (taken from realistic data), find the speed at which a `26 g` arrow is released, assuming that `70%` of the mechanical work done by the hand is actually transmitted to the arrow. (The other `30%` is lost to frictional heating inside the bow and kinetic energy of the recoiling and vibrating bow.) `sqrt`
25. A mass moving in one dimension is attached to a horizontal spring. It slides on the surface below it, with equal coefficients of static and kinetic friction, `mu_k=mu_s`. The equilibrium position is `x=0`. If the mass is pulled to some initial position and released from rest, it will complete some number of oscillations before friction brings it to a stop. When released from `x=a` `(a>0)`, it completes exactly 1/4 of an oscillation, i.e., it stops precisely at `x=0`. Similarly, define `b>0` as the greatest `x` from which it could be released and complete 1/2 of an oscillation, stopping on the far side and not coming back toward equilibrium. Find `b"/"a`. Hint: To keep the algebra simple, set every fixed parameter of the system equal to 1. `sqrt`
26. “Big wall” climbing is a specialized type of rock climbing that involves going up tall cliffs such as the ones in Yosemite, usually with the climbers spending at least one night sleeping on a natural ledge or an artificial “portaledge.” In this style of climbing, each pitch of the climb involves strenuously hauling up several heavy bags of gear --- a fact that has caused these climbs to be referred to as “vertical ditch digging.” (a) If an 80 kg haul bag has to be pulled up the full length of a 60 m rope, how much work is done? (b) Since it can be difficult to lift 80 kg, a 2:1 pulley is often used. The hauler then lifts the equivalent of 40 kg, but has to pull in 120 m of rope. How much work is done in this case? `sqrt`
13.8 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.