24.4 Induction by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
24.4 Induction
The principle of induction
Physicists of Michelson and Morley's generation thought that light was a mechanical vibration of the ether, but we now know that it is a ripple in the electric and magnetic fields. With hindsight, relativity essentially requires this:
- Relativity requires that changes in any field propagate as waves at a finite speed (p. 619).
- Relativity says that if a wave has a fixed speed but is not a mechanical disturbance in a physical medium, then it must travel at the universal velocity c (p. 683).
What is less obvious is that there are not two separate kinds of waves, electric and magnetic. In fact an electric wave can't exist without a magnetic one, or a magnetic one without an electric one. This new fact follows from the principle of induction, which was discovered experimentally by Faraday in 1831, seventy-five years before Einstein. Let's state Faraday's idea first, and then see how something like it must follow inevitably from relativity:
 the principle of induction
the principle of induction
Any electric field that changes over time will produce a magnetic field in the space around it.
Any magnetic field that changes over time will produce an electric field in the space around it.
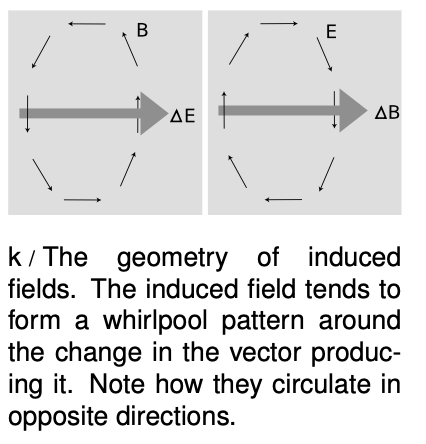
The induced field tends to have a whirlpool pattern, as shown in figure k, but the whirlpool image is not to be taken too literally; the principle of induction really just requires a field pattern such that, if one inserted a paddlewheel in it, the paddlewheel would spin. All of the field patterns shown in figure l are ones that could be created by induction; all have a counterclockwise “curl” to them.
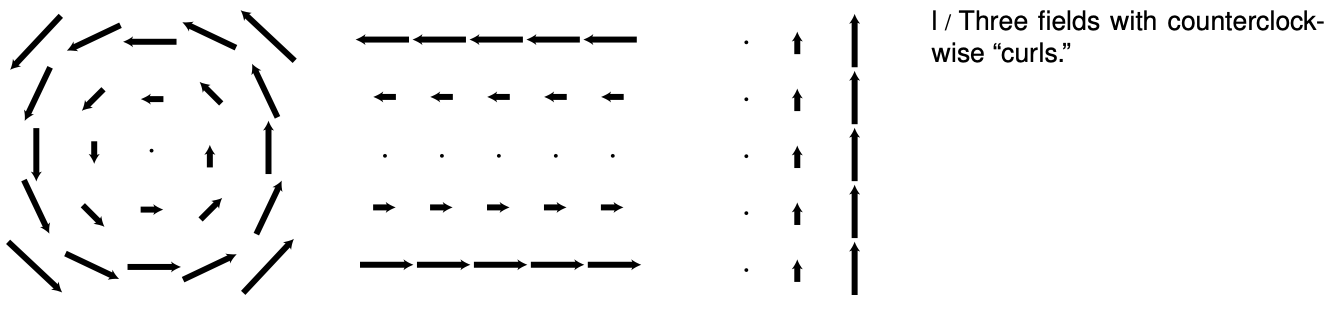

Figure m shows an example of the fundamental reason why a changing B field must create an E field. In section 23.2 we established that according to relativity, what one observer describes as a purely magnetic field, an observer in a different state of motion describes as a mixture of magnetic and electric fields. This is why there must be both an E and a B in observer 2's frame. Observer 2 cannot explain the electric field as coming from any charges. In frame 2, the E can only be explained as an effect caused by the changing B.
Observer 1 says, “2 feels a changing B field because he's moving through a static field.” Observer 2 says, “I feel a changing B because the magnet is getting closer.”
Although this argument doesn't prove the “whirlpool” geometry, we can verify that the fields I've drawn in figure m are consistent with it. The Δ vector is upward, and the electric field has a curliness to it: a paddlewheel inserted in the electric field would spin clockwise as seen from above, since the clockwise torque made by the strong electric field on the right is greater than the counterclockwise torque made by the weaker electric field on the left.
 Example 5: The generator
Example 5: The generator
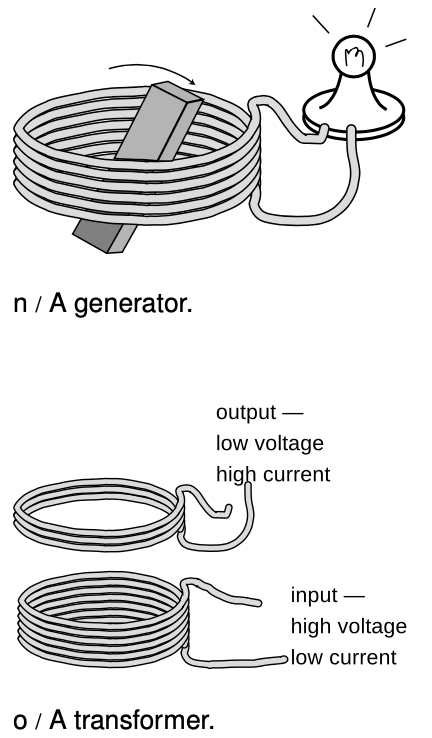
A generator, n, consists of a permanent magnet that rotates within a coil of wire. The magnet is turned by a motor or crank, (not shown). As it spins, the nearby magnetic field changes. According to the principle of induction, this changing magnetic field results in an electric field, which has a whirlpool pattern. This electric field pattern creates a current that whips around the coils of wire, and we can tap this current to light the lightbulb.
self-check:
When you're driving a car, the engine recharges the battery continuously using a device called an alternator, which is really just a generator like the one shown on the previous page, except that the coil rotates while the permanent magnet is fixed in place. Why can't you use the alternator to start the engine if your car's battery is dead?
(answer in the back of the PDF version of the book)
Example 6: The transformer
In example 18 on p. 593 we discussed the advantages of transmitting power over electrical lines using high voltages and low currents. However, we don't want our wall sockets to operate at 10000 volts! For this reason, the electric company uses a device called a transformer, o, to convert to lower voltages and higher currents inside your house. The coil on the input side creates a magnetic field. Transformers work with alternating current, so the magnetic field surrounding the input coil is always changing. This induces an electric field, which drives a current around the output coil.
If both coils were the same, the arrangement would be symmetric, and the output would be the same as the input, but an output coil with a smaller number of coils gives the electric forces a smaller distance through which to push the electrons. Less mechanical work per unit charge means a lower voltage. Conservation of energy, however, guarantees that the amount of power on the output side must equal the amount put in originally, I_"in"V_"in"=I_"out"V_"out", so this reduced voltage must be accompanied by an increased current.
24.4 Induction by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.