1.2 Scaling of area and volume by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

1.2 Scaling of area and volume

Great fleas have lesser fleas
 Upon their backs to bite 'em.
 And lesser fleas have lesser still,
 And so ad infinitum. -- Jonathan Swift

Now how do these conversions of area and volume relate to the questions I posed about sizes of living things? Well, imagine that you are shrunk like Alice in Wonderland to the size of an insect. One way of thinking about the change of scale is that what used to look like a centimeter now looks like perhaps a meter to you, because you're so much smaller. If area and volume scaled according to most people's intuitive, incorrect expectations, with 1` "m"^2` being the same as 100 `"cm"^2`, then there would be no particular reason why nature should behave any differently on your new, reduced scale. But nature does behave differently now that you're small. For instance, you will find that you can walk on water, and jump to many times your own height. The physicist Galileo Galilei had the basic insight that the scaling of area and volume determines how natural phenomena behave differently on different scales. He first reasoned about mechanical structures, but later extended his insights to living things, taking the then-radical point of view that at the fundamental level, a living organism should follow the same laws of nature as a machine. We will follow his lead by first discussing machines and then living things.

Galileo on the behavior of nature on large and small scales

One of the world's most famous pieces of scientific writing is Galileo's Dialogues Concerning the Two New Sciences. Galileo was an entertaining writer who wanted to explain things clearly to laypeople, and he livened up his work by casting it in the form of a dialogue among three people. Salviati is really Galileo's alter ego. Simplicio is the stupid character, and one of the reasons Galileo got in trouble with the Church was that there were rumors that Simplicio represented the Pope. Sagredo is the earnest and intelligent student, with whom the reader is supposed to identify. (The following excerpts are from the 1914 translation by Crew and de Salvio.)

SAGREDO: Yes, that is what I mean; and I refer especially to his last assertion which I have always regarded as false...; namely, that in speaking of these and other similar machines one cannot argue from the small to the large, because many devices which succeed on a small scale do not work on a large scale. Now, since mechanics has its foundations in geometry, where mere size [ is unimportant], I do not see that the properties of circles, triangles, cylinders, cones and other solid figures will change with their size.

 If, therefore, a large machine be constructed in such a way that its parts bear to one another the same ratio as in a smaller one, and if the smaller is sufficiently strong for the purpose for which it is designed, I do not see why the larger should not be able to withstand any severe and destructive tests to which it may be subjected.

Salviati contradicts Sagredo:

SALVIATI: ... Please observe, gentlemen, how facts which at first seem improbable will, even on scant explanation, drop the cloak which has hidden them and stand forth in naked and simple beauty. Who does not know that a horse falling from a height of three or four cubits will break his bones, while a dog falling from the same height or a cat from a height of eight or ten cubits will suffer no injury? Equally harmless would be the fall of a grasshopper from a tower or the fall of an ant from the distance of the moon.

The point Galileo is making here is that small things are sturdier in proportion to their size. There are a lot of objections that could be raised, however. After all, what does it really mean for something to be “strong”, to be “strong in proportion to its size,” or to be strong “out of proportion to its size?” Galileo hasn't given operational definitions of things like “strength,” i.e., definitions that spell out how to measure them numerically.

Also, a cat is shaped differently from a horse --- an enlarged photograph of a cat would not be mistaken for a horse, even if the photo-doctoring experts at the National Inquirer made it look like a person was riding on its back. A grasshopper is not even a mammal, and it has an exoskeleton instead of an internal skeleton. The whole argument would be a lot more convincing if we could do some isolation of variables, a scientific term that means to change only one thing at a time, isolating it from the other variables that might have an effect. If size is the variable whose effect we're interested in seeing, then we don't really want to compare things that are different in size but also different in other ways.

SALVIATI: ... we asked the reason why [shipbuilders] employed stocks, scaffolding, and bracing of larger dimensions for launching a big vessel than they do for a small one; and [an old man] answered that they did this in order to avoid the danger of the ship parting under its own heavy weight, a danger to which small boats are not subject?

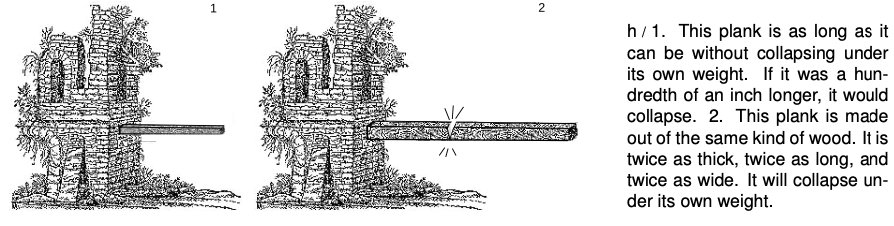
Also, Galileo is doing something that would be frowned on in modern science: he is mixing experiments whose results he has actually observed (building boats of different sizes), with experiments that he could not possibly have done (dropping an ant from the height of the moon). He now relates how he has done actual experiments with such planks, and found that, according to this operational definition, they are not strong in proportion to their sizes. The larger one breaks. He makes sure to tell the reader how important the result is, via Sagredo's astonished response:

In other words, this specific experiment, using things like wooden planks that have no intrinsic scientific interest, has very wide implications because it points out a general principle, that nature acts differently on different scales.

To finish the discussion, Galileo gives an explanation. He says that the strength of a plank (defined as, say, the weight of the heaviest boulder you could put on the end without breaking it) is proportional to its cross-sectional area, that is, the surface area of the fresh wood that would be exposed if you sawed through it in the middle. Its weight, however, is proportional to its volume.¹

How do the volume and cross-sectional area of the longer plank compare with those of the shorter plank? We have already seen, while discussing conversions of the units of area and volume, that these quantities don't act the way most people naively expect. You might think that the volume and area of the longer plank would both be doubled compared to the shorter plank, so they would increase in proportion to each other, and the longer plank would be equally able to support its weight. You would be wrong, but Galileo knows that this is a common misconception, so he has Salviati address the point specifically:

SALVIATI: ... Take, for example, a cube two inches on a side so that each face has an area of four square inches and the total area, i.e., the sum of the six faces, amounts to twenty-four square inches; now imagine this cube to be sawed through three times [with cuts in three perpendicular planes] so as to divide it into eight smaller cubes, each one inch on the side, each face one inch square, and the total surface of each cube six square inches instead of twenty-four in the case of the larger cube. It is evident therefore, that the surface of the little cube is only one-fourth that of the larger, namely, the ratio of six to twenty-four; but the volume of the solid cube itself is only one-eighth; the volume, and hence also the weight, diminishes therefore much more rapidly than the surface... You see, therefore, Simplicio, that I was not mistaken when ... I said that the surface of a small solid is comparatively greater than that of a large one.

The same reasoning applies to the planks. Even though they are not cubes, the large one could be sawed into eight small ones, each with half the length, half the thickness, and half the width. The small plank, therefore, has more surface area in proportion to its weight, and is therefore able to support its own weight while the large one breaks.

You probably are not going to believe Galileo's claim that this has deep implications for all of nature unless you can be convinced that the same is true for any shape. Every drawing you've seen so far has been of squares, rectangles, and rectangular solids. Clearly the reasoning about sawing things up into smaller pieces would not prove anything about, say, an egg, which cannot be cut up into eight smaller egg-shaped objects with half the length.

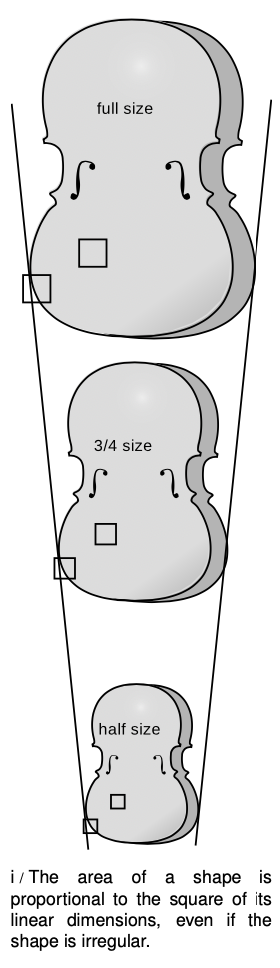
Is it always true that something half the size has one quarter the surface area and one eighth the volume, even if it has an irregular shape? Take the example of a child's violin. Violins are made for small children in smaller size to accommodate their small bodies. Figure i shows a full-size violin, along with two violins made with half and 3/4 of the normal length.² Let's study the surface area of the front panels of the three violins.

Consider the square in the interior of the panel of the full-size violin. In the 3/4-size violin, its height and width are both smaller by a factor of 3/4, so the area of the corresponding, smaller square becomes 3/4×3/4=9/16 of the original area, not 3/4 of the original area. Similarly, the corresponding square on the smallest violin has half the height and half the width of the original one, so its area is 1/4 the original area, not half.

The same reasoning works for parts of the panel near the edge, such as the part that only partially fills in the other square. The entire square scales down the same as a square in the interior, and in each violin the same fraction (about 70%) of the square is full, so the contribution of this part to the total area scales down just the same.

Since any small square region or any small region covering part of a square scales down like a square object, the entire surface area of an irregularly shaped object changes in the same manner as the surface area of a square: scaling it down by 3/4 reduces the area by a factor of 9/16, and so on.

In general, we can see that any time there are two objects with the same shape, but different linear dimensions (i.e., one looks like a reduced photo of the other), the ratio of their areas equals the ratio of the squares of their linear dimensions:

`A_1/A_2=(L_1/ L_2)^2`.

Note that it doesn't matter where we choose to measure the linear size, `L`, of an object. In the case of the violins, for instance, it could have been measured vertically, horizontally, diagonally, or even from the bottom of the left f-hole to the middle of the right f-hole. We just have to measure it in a consistent way on each violin. Since all the parts are assumed to shrink or expand in the same manner, the ratio `L_1"/"L_2` is independent of the choice of measurement.

It is also important to realize that it is completely unnecessary to have a formula for the area of a violin. It is only possible to derive simple formulas for the areas of certain shapes like circles, rectangles, triangles and so on, but that is no impediment to the type of reasoning we are using.

Sometimes it is inconvenient to write all the equations in terms of ratios, especially when more than two objects are being compared. A more compact way of rewriting the previous equation is

A ∝L².

The symbol “`alpha`"  means “is proportional to.” Scientists and engineers often speak about such relationships verbally using the phrases “scales like” or “goes like,” for instance “area goes like length squared.”

All of the above reasoning works just as well in the case of volume. Volume goes like length cubed:

V ∝ L³.

self-check: When a car or truck travels over a road, there is wear and tear on the road surface, which incurs a cost. Studies show that the cost `C` per kilometer of travel is related to the weight per axle `w` by `C alpha w^4`. Translate this into a statement about ratios.

(answer in the back of the PDF version of the book)

If different objects are made of the same material with the same density, `rho=M"/"V`, then their masses, `M=rho*V`, are proportional to L³. (The symbol for density is `rho`, the lower-case Greek letter “rho.”)

An important point is that all of the above reasoning about scaling only applies to objects that are the same shape. For instance, a piece of paper is larger than a pencil, but has a much greater surface-to-volume ratio.

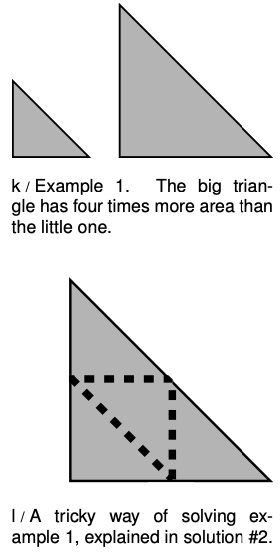Example 1: Scaling of the area of a triangle

`=>` In figure k, the larger triangle has sides twice as long. How many times greater is its area?

Correct solution #1: Area scales in proportion to the square of the linear dimensions, so the larger triangle has four times more area `(2^2=4)` .

Correct solution #2: You could cut the larger triangle into four of the smaller size, as shown in fig. (b), so its area is four times greater. (This solution is correct, but it would not work for a shape like a circle, which can't be cut up into smaller circles.)

Correct solution #3: The area of a triangle is given by

`A=1/2*b*h`, where `b`is the base and `h` is the height. The areas of the triangles are

             `A_1=b_1h_1"/"2`
             `A_2=b_2h_2"/"2`
                   `=(2b_1)(2h_1)"/"2`
                  `=2b_1h_1`
 `A_2"/"A_1`=`(2b_1h_1)"/"(b_1h_1"/"2)`
                  `=4`

(Although this solution is correct, it is a lot more work than solution #1, and it can only be used in this case because a triangle is a simple geometric shape, and we happen to know a formula for its area.)

Correct solution #4: The area of a triangle is `A=bh"/"2`. The comparison of the areas will come out the same as long as the ratios of the linear sizes of the triangles is as specified, so let's just say `b_1=1.00 "m"` and `b_2=2.00 "m"`. The heights are then also `h_1=100 "m"` and `h_2=2.00 "m"`, giving areas `A_1=0.50 "m"^2` and `A_2=2.00 "m"^2`, so `A_2"/"A_1=4.00.`

(The solution is correct, but it wouldn't work with a shape for whose area we don't have a formula. Also, the numerical calculation might make the answer of `4.00` appear inexact, whereas solution #1 makes it clear that it is exactly `4`.)

Incorrect solution: The area of a triangle is  `A=bh"/"2`, and if you plug in `b=2.00 "m"` and `h=2.00 "m"`, you get `A=2.00 "m"^2`, so the bigger triangle has `2.00` times more area. (This solution is incorrect because no comparison has been made with the smaller triangle.)

Example 2: Scaling of the volume of a sphere

`=>` In figure m, the larger sphere has a radius that is five times greater. How many times greater is its volume?

Correct solution #1: Volume scales like the third power of the linear size, so the larger sphere has a volume that is 125 times greater (53=125).

Correct solution #2: The volume of a sphere is `V =(4/3)pir^3`, so

         `V_1=4/3pir_1^3`
         `V_2=4/3pir_2^3`
              `=4/3pi(5r_1)^3`
              `=500/3pir_1^3`
`V_2"/"V_1`=`(500/3pir_1^3)"/"(4/3pir_1^3)=125`

Incorrect solution: The volume of a sphere is `V=(4"/"3)pir^3`, so

         `V_1=4"/"3pir_1^3`
         `V_2=4"/"3pir_2^3`
              `=4"/"3pi*5r_1^3`
              `=20"/"3pir_1^3`
`V_2"/"V_1`=`(20/3pir_1^3)"/"(4/3pir_1^3)=5`

(The solution is incorrect because `(5r_1)^3` is not the same as `5r_1^3`.)

Example 3: Scaling of a more complex shape

`=>` The first letter “S” in figure n is in a 36-point font, the second in 48-point. How many times more ink is required to make the larger “S”? (Points are a unit of length used in typography.)

Correct solution: The amount of ink depends on the area to be covered with ink, and area is proportional to the square of the linear dimensions, so the amount of ink required for the second “S” is greater by a factor of `(48"/"36)^2=1.78`.

Incorrect solution: The length of the curve of the second “S” is longer by a factor of `48"/"36=1.33`, so `1.33` times more ink is required.

(The solution is wrong because it assumes incorrectly that the width of the curve is the same in both cases. Actually both the width and the length of the curve are greater by a factor of `48"/"36`, so the area is greater by a factor of `(48"/"36)^2=1.78`.)

Reasoning about ratios and proportionalities is one of the three essential mathematical skills, summarized on pp.532-533, that you need for success in this course.

`=>` Solved problem: a telescope gathers light — problem 11

`=>` Solved problem: distance from an earthquake — problem 12

Discussion Questions

A   A toy fire engine is 1/30 the size of the real one, but is constructed from the same metal with the same proportions. How many times smaller is its weight? How many times less red paint would be needed to paint it?

B   Galileo spends a lot of time in his dialog discussing what really happens when things break. He discusses everything in terms of Aristotle's now-discredited explanation that things are hard to break, because if something breaks, there has to be a gap between the two halves with nothing in between, at least initially. Nature, according to Aristotle, “abhors a vacuum,” i.e., nature doesn't “like” empty space to exist. Of course, air will rush into the gap immediately, but at the very moment of breaking, Aristotle imagined a vacuum in the gap. Is Aristotle's explanation of why it is hard to break things an experimentally testable statement? If so, how could it be tested experimentally?

1.2 Scaling of area and volume by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.