19.5 The Doppler effect by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
19.5 The Doppler effect
Figure `v` shows the wave pattern made by the tip of a vibrating rod which is moving across the water. If the rod had been vibrating in one place, we would have seen the familiar pattern of concentric circles, all centered on the same point. But since the source of the waves is moving, the wavelength is shortened on one side and lengthened on the other. This is known as the Doppler effect.
Note that the velocity of the waves is a fixed property of the medium, so for example the forward-going waves do not get an extra boost in speed as would a material object like a bullet being shot forward from an airplane.
We can also infer a change in frequency. Since the velocity is constant, the equation `v=flambda` tells us that the change in wavelength must be matched by an opposite change in frequency: higher frequency for the waves emitted forward, and lower for the ones emitted backward. The frequency Doppler effect is the reason for the familiar dropping-pitch sound of a race car going by. As the car approaches us, we hear a higher pitch, but after it passes us we hear a frequency that is lower than normal.
The Doppler effect will also occur if the observer is moving but the source is stationary. For instance, an observer moving toward a stationary source will perceive one crest of the wave, and will then be surrounded by the next crest sooner than she otherwise would have, because she has moved toward it and hastened her encounter with it. Roughly speaking, the Doppler effect depends only the relative motion of the source and the observer, not on their absolute state of motion (which is not a well-defined notion in physics) or on their velocity relative to the medium.
Restricting ourselves to the case of a moving source, and to waves emitted either directly along or directly against the direction of motion, we can easily calculate the wavelength, or equivalently the frequency, of the Doppler-shifted waves. Let `v` be the velocity of the waves, and `v_s` the velocity of the source. The wavelength of the forward-emitted waves is shortened by an amount `v_sT` equal to the distance traveled by the source over the course of one period. Using the definition`f=1`/`T` and the equation `v=flambda`, we find for the wavelength of the Doppler-shifted wave the equation `lambda'=(1-v_s/v)lambda`.
A similar equation can be used for the backward-emitted waves, but with a plus sign rather than a minus sign.
Example 6: Doppler-shifted sound from a race car
- If a race car moves at a velocity of 50 m/s, and the velocity of sound is 340 m/s, by what percentage are the wavelength and frequency of its sound waves shifted for an observer lying along its line of motion?
- For an observer whom the car is approaching, we find
`1-v_s`/`v=0.85`,
so the shift in wavelength is 15%. Since the frequency is inversely proportional to the wavelength for a fixed value of the speed of sound, the frequency is shifted upward by
`(1`/`0.85)=1.18`,
i.e., a change of 18%. (For velocities that are small compared to the wave velocities, the Doppler shifts of the wavelength and frequency are about the same.)
Example 7: Doppler shift of the light emitted by a race car
- What is the percent shift in the wavelength of the light waves emitted by a race car's headlights?
- Looking up the speed of light, `v=3.0×10^8 m`/`s`, we find
`1-v_s`/`v=0.99999983`,
i.e., the percentage shift is only 0.000017%.
The second example shows that under ordinary earthbound circumstances, Doppler shifts of light are negligible because ordinary things go so much slower than the speed of light. It's a different story, however, when it comes to stars and galaxies, and this leads us to a story that has profound implications for our understanding of the origin of the universe.
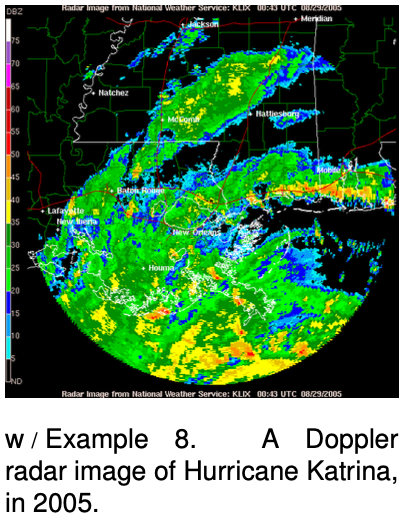Example 8: Doppler radar
The first use of radar was by Britain during World War II: antennas on the ground sent radio waves up into the sky, and detected the echoes when the waves were reflected from German planes. Later, air forces wanted to mount radar antennas on airplanes, but then there was a problem, because if an airplane wanted to detect another airplane at a lower altitude, it would have to aim its radio waves downward, and then it would get echoes from the ground. The solution was the invention of Doppler radar, in which echoes from the ground were differentiated from echoes from other aircraft according to their Doppler shifts. A similar technology is used by meteorologists to map out rainclouds without being swamped by reflections from the ground, trees, and buildings.
Optional topic: Doppler shifts of light
If Doppler shifts depend only on the relative motion of the source and receiver, then there is no way for a person moving with the source and another person moving with the receiver to determine who is moving and who isn't. Either can blame the Doppler shift entirely on the other's motion and claim to be at rest herself. This is entirely in agreement with the principle stated originally by Galileo that all motion is relative.
On the other hand, a careful analysis of the Doppler shifts of water or sound waves shows that it is only approximately true, at low speeds, that the shifts just depend on the relative motion of the source and observer. For instance, it is possible for a jet plane to keep up with its own sound waves, so that the sound waves appear to stand still to the pilot of the plane. The pilot then knows she is moving at exactly the speed of sound. The reason this doesn't disprove the relativity of motion is that the pilot is not really determining her absolute motion but rather her motion relative to the air, which is the medium of the sound waves.
Einstein realized that this solved the problem for sound or water waves, but would not salvage the principle of relative motion in the case of light waves, since light is not a vibration of any physical medium such as water or air. Beginning by imagining what a beam of light would look like to a person riding a motorcycle alongside it, Einstein eventually came up with a radical new way of describing the universe, in which space and time are distorted as measured by observers in different states of motion. As a consequence of this theory of relativity, he showed that light waves would have Doppler shifts that would exactly, not just approximately, depend only on the relative motion of the source and receiver. The resolution of the motorcycle paradox is given in example 7 on p. 690, and a quantitative discussion of Doppler shifts of light is given on p. 694.
The Big Bang
As soon as astronomers began looking at the sky through telescopes, they began noticing certain objects that looked like clouds in deep space. The fact that they looked the same night after night meant that they were beyond the earth's atmosphere. Not knowing what they really were, but wanting to sound official, they called them “nebulae,” a Latin word meaning “clouds” but sounding more impressive. In the early 20th century, astronomers realized that although some really were clouds of gas (e.g., the middle “star” of Orion's sword, which is visibly fuzzy even to the naked eye when conditions are good), others were what we now call galaxies: virtual island universes consisting of trillions of stars (for example the Andromeda Galaxy, which is visible as a fuzzy patch through binoculars). Three hundred years after Galileo had resolved the Milky Way into individual stars through his telescope, astronomers realized that the universe is made of galaxies of stars, and the Milky Way is simply the visible part of the flat disk of our own galaxy, seen from inside.
This opened up the scientific study of cosmology, the structure and history of the universe as a whole, a field that had not been seriously attacked since the days of Newton. Newton had realized that if gravity was always attractive, never repulsive, the universe would have a tendency to collapse. His solution to the problem was to posit a universe that was infinite and uniformly populated with matter, so that it would have no geometrical center. The gravitational forces in such a universe would always tend to cancel out by symmetry, so there would be no collapse. By the 20th century, the belief in an unchanging and infinite universe had become conventional wisdom in science, partly as a reaction against the time that had been wasted trying to find explanations of ancient geological phenomena based on catastrophes suggested by biblical events like Noah's flood.
In the 1920's astronomer Edwin Hubble began studying the Doppler shifts of the light emitted by galaxies. A former college football player with a serious nicotine addiction, Hubble did not set out to change our image of the beginning of the universe. His autobiography seldom even mentions the cosmological discovery for which he is now remembered. When astronomers began to study the Doppler shifts of galaxies, they expected that each galaxy's direction and velocity of motion would be essentially random. Some would be approaching us, and their light would therefore be Doppler-shifted to the blue end of the spectrum, while an equal number would be expected to have red shifts. What Hubble discovered instead was that except for a few very nearby ones, all the galaxies had red shifts, indicating that they were receding from us at a hefty fraction of the speed of light. Not only that, but the ones farther away were receding more quickly. The speeds were directly proportional to their distance from us.
Did this mean that the earth (or at least our galaxy) was the center of the universe? No, because Doppler shifts of light only depend on the relative motion of the source and the observer. If we see a distant galaxy moving away from us at 10% of the speed of light, we can be assured that the astronomers who live in that galaxy will see ours receding from them at the same speed in the opposite direction. The whole universe can be envisioned as a rising loaf of raisin bread. As the bread expands, there is more and more space between the raisins. The farther apart two raisins are, the greater the speed with which they move apart.
Extrapolating backward in time using the known laws of physics, the universe must have been denser and denser at earlier and earlier times. At some point, it must have been extremely dense and hot, and we can even detect the radiation from this early fireball, in the form of microwave radiation that permeates space. The phrase Big Bang was originally coined by the doubters of the theory to make it sound ridiculous, but it stuck, and today essentially all astronomers accept the Big Bang theory based on the very direct evidence of the red shifts and the cosmic microwave background radiation.
What the Big Bang is not
Finally it should be noted what the Big Bang theory is not. It is not an explanation of why the universe exists. Such questions belong to the realm of religion, not science. Science can find ever simpler and ever more fundamental explanations for a variety of phenomena, but ultimately science takes the universe as it is according to observations.
Furthermore, there is an unfortunate tendency, even among many scientists, to speak of the Big Bang theory as a description of the very first event in the universe, which caused everything after it. Although it is true that time may have had a beginning (Einstein's theory of general relativity admits such a possibility), the methods of science can only work within a certain range of conditions such as temperature and density. Beyond a temperature of about `109` degrees C, the random thermal motion of subatomic particles becomes so rapid that its velocity is comparable to the speed of light. Early enough in the history of the universe, when these temperatures existed, Newtonian physics becomes less accurate, and we must describe nature using the more general description given by Einstein's theory of relativity, which encompasses Newtonian physics as a special case. At even higher temperatures, beyond about `1033` degrees, physicists know that Einstein's theory as well begins to fall apart, but we don't know how to construct the even more general theory of nature that would work at those temperatures. No matter how far physics progresses, we will never be able to describe nature at infinitely high temperatures, since there is a limit to the temperatures we can explore by experiment and observation in order to guide us to the right theory. We are confident that we understand the basic physics involved in the evolution of the universe starting a few minutes after the Big Bang, and we may be able to push back to milliseconds or microseconds after it, but we cannot use the methods of science to deal with the beginning of time itself.
Discussion Questions
A If an airplane travels at exactly the speed of sound, what would be the wavelength of the forward-emitted part of the sound waves it emitted? How should this be interpreted, and what would actually happen? What happens if it's going faster than the speed of sound? Can you use this to explain what you see in figure aa?
B If bullets go slower than the speed of sound, why can a supersonic fighter plane catch up to its own sound, but not to its own bullets?
C If someone inside a plane is talking to you, should their speech be Doppler shifted?
D The plane in figure ab was photographed when it was traveling at a speed close to the speed of sound. Comparing figures aa and ab, how can we tell from the angles of the cones that the speed is much lower in figure ab?
19.5 The Doppler effect by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.