26.3 The electron by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
26.3 The electron
Cathode rays
One such parlor trick was the cathode ray. To produce it, you first had to hire a good glassblower and find a good vacuum pump. The glassblower would create a hollow tube and embed two pieces of metal in it, called the electrodes, which were connected to the outside via metal wires passing through the glass. Before letting him seal up the whole tube, you would hook it up to a vacuum pump, and spend several hours huffing and puffing away at the pump's hand crank to get a good vacuum inside. Then, while you were still pumping on the tube, the glassblower would melt the glass and seal the whole thing shut. Finally, you would put a large amount of positive charge on one wire and a large amount of negative charge on the other. Metals have the property of letting charge move through them easily, so the charge deposited on one of the wires would quickly spread out because of the repulsion of each part of it for every other part. This spreading-out process would result in nearly all the charge ending up in the electrodes, where there is more room to spread out than there is in the wire. For obscure historical reasons a negative electrode is called a cathode and a positive one is an anode.
Figure g shows the light-emitting stream that was observed. If, as shown in this figure, a hole was made in the anode, the beam would extend on through the hole until it hit the glass. Drilling a hole in the cathode, however would not result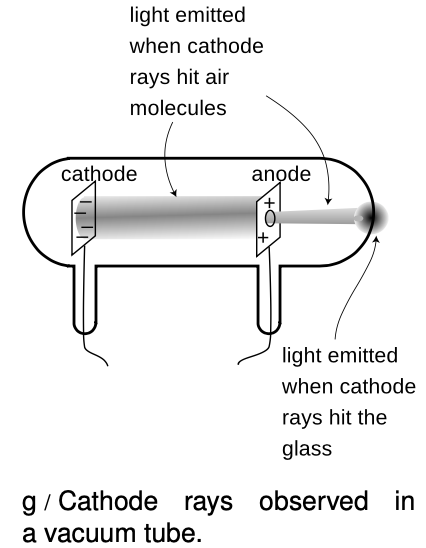 
in any beam coming out on the left side, and this indicated that the stuff, whatever it was, was coming from the cathode. The rays were therefore christened “cathode rays.” (The terminology is still used today in the term “cathode ray tube” or “CRT” for the picture tube of a TV or computer monitor.)
Were cathode rays a form of light, or of matter?
Were cathode rays a form of light, or matter? At first no one really cared what they were, but as their scientific importance became more apparent, the light-versus-matter issue turned into a controversy along nationalistic lines, with the Germans advocating light and the English holding out for matter. The supporters of the material interpretation imagined the rays as consisting of a stream of atoms ripped from the substance of the cathode.
One of our defining characteristics of matter is that material objects cannot pass through each other. Experiments showed that cathode rays could penetrate at least some small thickness of matter, such as a metal foil a tenth of a millimeter thick, implying that they were a form of light.
Other experiments, however, pointed to the contrary conclusion. Light is a wave phenomenon, and one distinguishing property of waves is demonstrated by speaking into one end of a paper towel roll. The sound waves do not emerge from the other end of the tube as a focused beam. Instead, they begin spreading out in all directions as soon as they emerge. This shows that waves do not necessarily travel in straight lines. If a piece of metal foil in the shape of a star or a cross was placed in the way of the cathode ray, then a “shadow” of the same shape would appear on the glass, showing that the rays traveled in straight lines. This straight-line motion suggested that they were a stream of small particles of matter.
These observations were inconclusive, so what was really needed was a determination of whether the rays had mass and weight. The trouble was that cathode rays could not simply be collected in a cup and put on a scale. When the cathode ray tube is in operation, one does not observe any loss of material from the cathode, or any crust being deposited on the anode.
Nobody could think of a good way to weigh cathode rays, so the next most obvious way of settling the light/matter debate was to check whether the cathode rays possessed electrical charge. Light was known to be uncharged. If the cathode rays carried charge, they were definitely matter and not light, and they were presumably being made to jump the gap by the simultaneous repulsion of the negative charge in the cathode and attraction of the positive charge in the anode. The rays would overshoot the anode because of their momentum. (Although electrically charged particles do not normally leap across a gap of vacuum, very large amounts of charge were being used, so the forces were unusually intense.)
Thomson's experiments
Physicist J.J. Thomson at Cambridge carried out a series of definitive experiments on cathode rays around the year 1897. By turning them slightly off course with electrical forces, i, he showed that they were indeed electrically charged, which was strong evidence that they were material. Not only that, but he proved that they had mass, and measured the ratio of their mass to their charge, `m"/"q`. Since their mass was not zero, he concluded that they were a form of matter, and presumably made up of a stream of microscopic, negatively charged particles. When Millikan published his results fourteen years later, it was reasonable to assume that the charge of one such particle equaled minus one fundamental charge, `q=-e`, and from the combination of Thomson's and Millikan's results one could therefore determine the mass of a single cathode ray particle.
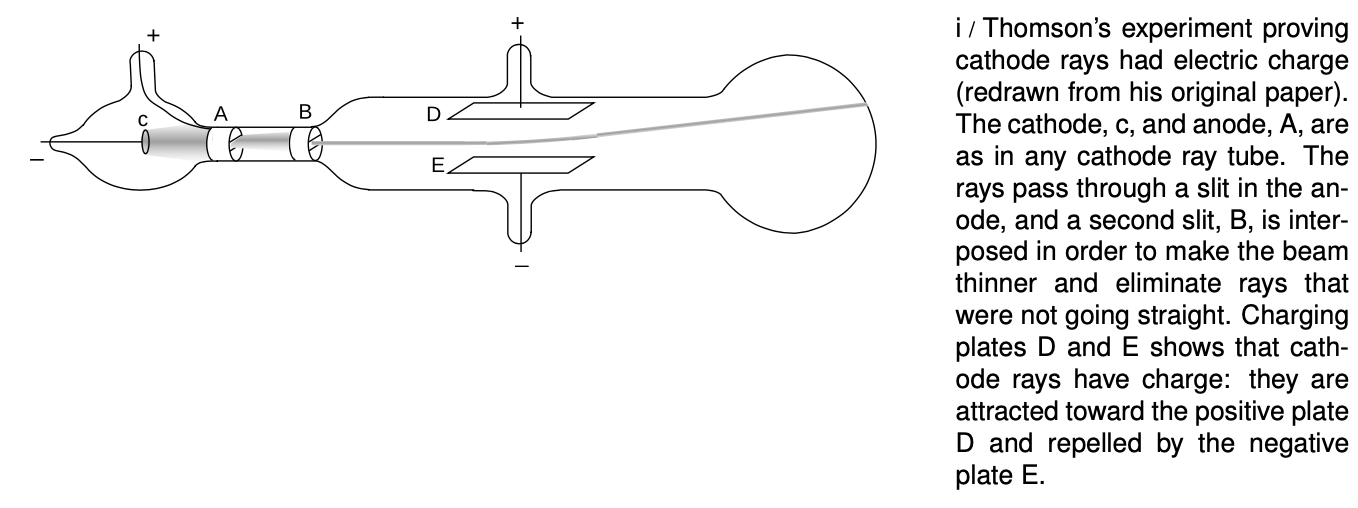
The basic technique for determining `m"/"q` was simply to measure the angle through which the charged plates bent the beam. The electric force acting on a cathode ray particle while it was between the plates was
By Newton's second law, , we can find `m/q`:
`m/q=E/a`
There was just one catch. Thomson needed to know the cathode ray particles' velocity in order to figure out their acceleration. At that point, however, nobody had even an educated guess as to the speed of the cathode rays produced in a given vacuum tube. The beam appeared to leap across the vacuum tube practically instantaneously, so it was no simple matter of timing it with a stopwatch!
Thomson's clever solution was to observe the effect of both electric and magnetic forces on the beam. The magnetic force exerted by a particular magnet would depend on both the cathode ray's charge and its speed:
Thomson played with the electric and magnetic forces until either one would produce an equal effect on the beam, allowing him to solve for the speed,
Knowing the speed (which was on the order of 10% of the speed of light for his setup), he was able to find the acceleration and thus the mass-to-charge ratio `m"/"q`. Thomson's techniques were relatively crude (or perhaps more charitably we could say that they stretched the state of the art of the time), so with various methods he came up with `m"/"q` values that ranged over about a factor of two, even for cathode rays extracted from a cathode made of a single material. The best modern value is `m"/"q=5.69×10^(-12) kg"/"C`, which is consistent with the low end of Thomson's range.
The cathode ray as a subatomic particle: the electron
What was significant about Thomson's experiment was not the actual numerical value of `m"/"q`, however, so much as the fact that, combined with Millikan's value of the fundamental charge, it gave a mass for the cathode ray particles that was thousands of times smaller than the mass of even the lightest atoms. Even without Millikan's results, which were 14 years in the future, Thomson recognized that the cathode rays' `m"/"q` was thousands of times smaller than the `m"/"q` ratios that had been measured for electrically charged atoms in chemical solutions. He correctly interpreted this as evidence that the cathode rays were smaller building blocks --- he called themelectrons --- out of which atoms themselves were formed. This was an extremely radical claim, coming at a time when atoms had not yet been proven to exist! Even those who used the word “atom” often considered them no more than mathematical abstractions, not literal objects. The idea of searching for structure inside of “unsplittable” atoms was seen by some as lunacy, but within ten years Thomson's ideas had been amply verified by many more detailed experiments.
Discussion Questions
A Thomson started to become convinced during his experiments that the “cathode rays” observed coming from the cathodes of vacuum tubes were building blocks of atoms --- what we now call electrons. He then carried out observations with cathodes made of a variety of metals, and found that `m"/"q` was roughly the same in every case, considering his limited accuracy. Given his suspicion, why did it make sense to try different metals? How would the consistent values of `m"/"q` test his hypothesis?
B My students have frequently asked whether the `m"/"q` that Thomson measured was the value for a single electron, or for the whole beam. Can you answer this question?
C Thomson found that the `m"/"q` of an electron was thousands of times smaller than that of charged atoms in chemical solutions. Would this imply that the electrons had more charge? Less mass? Would there be no way to tell? Explain. Remember that Millikan's results were still many years in the future, so `q` was unknown.
D Can you guess any practical reason why Thomson couldn't just let one electron fly across the gap before disconnecting the battery and turning off the beam, and then measure the amount of charge deposited on the anode, thus allowing him to measure the charge of a single electron directly?
E Why is it not possible to determine `m` and `q` themselves, rather than just their ratio, by observing electrons' motion in electric and magnetic fields?
The raisin cookie model
Based on his experiments, Thomson proposed a picture of the atom which became known as the raisin cookie model. In the neutral atom, j, there are four electrons with a total charge of `-4e`, sitting in a sphere (the “cookie”) with a charge of `+4e` spread throughout it. It was known that chemical reactions could not change one element into another, so in Thomson's scenario, each element's cookie sphere had a permanently fixed radius, mass, and positive charge, different from those of other elements. The electrons, however, were not a permanent feature of the atom, and could be tacked on or pulled out to make charged ions. Although we now know, for instance, that a neutral atom with four electrons is the element beryllium, scientists at the time did not know how many electrons the various neutral atoms possessed.
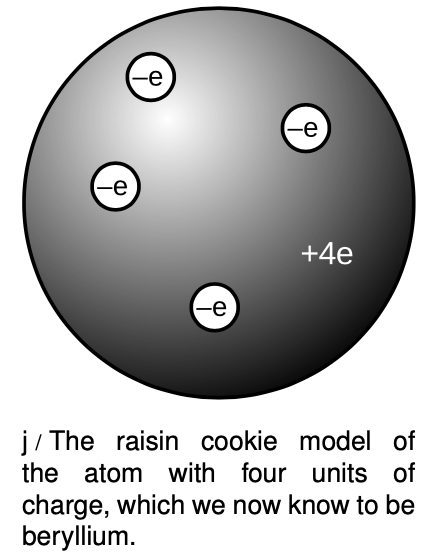This model is clearly different from the one you've learned in grade school or through popular culture, where the positive charge is concentrated in a tiny nucleus at the atom's center. An equally important change in ideas about the atom has been the realization that atoms and their constituent subatomic particles behave entirely differently from objects on the human scale. For instance, we'll see later that an electron can be in more than one place at one time. The raisin cookie model was part of a long tradition of attempts to make mechanical models of phenomena, and Thomson and his contemporaries never questioned the appropriateness of building a mental model of an atom as a machine with little parts inside. Today, mechanical models of atoms are still used (for instance the tinker-toy-style molecular modeling kits like the ones used by Watson and Crick to figure out the double helix structure of DNA), but scientists realize that the physical objects are only aids to help our brains' symbolic and visual processes think about atoms.
Although there was no clear-cut experimental evidence for many of the details of the raisin cookie model, physicists went ahead and started working out its implications. For instance, suppose you had a four-electron atom. All four electrons would be repelling each other, but they would also all be attracted toward the center of the “cookie” sphere. The result should be some kind of stable, symmetric arrangement in which all the forces canceled out. People sufficiently clever with math soon showed that the electrons in a four-electron atom should settle down at the vertices of a pyramid with one less side than the Egyptian kind, i.e., a regular tetrahedron. This deduction turns out to be wrong because it was based on incorrect features of the model, but the model also had many successes, a few of which we will now discuss.
Example 1: Flow of electrical charge in wires
One of my former students was the son of an electrician, and had become an electrician himself. He related to me how his father had remained refused to believe all his life that electrons really flowed through wires. If they had, he reasoned, the metal would have gradually become more and more damaged, eventually crumbling to dust.
His opinion is not at all unreasonable based on the fact that electrons are material particles, and that matter cannot normally pass through matter without making a hole through it. Nineteenth-century physicists would have shared his objection to a charged-particle model of the flow of electrical charge. In the raisin-cookie model, however, the electrons are very low in mass, and therefore presumably very small in size as well. It is not surprising that they can slip between the atoms without damaging them.
Example 2: Flow of electrical charge across cell membranes
Your nervous system is based on signals carried by charge moving from nerve cell to nerve cell. Your body is essentially all liquid, and atoms in a liquid are mobile. This means that, unlike the case of charge flowing in a solid wire, entire charged atoms can flow in your nervous system
Example 3: Emission of electrons in a cathode ray tube
Why do electrons detach themselves from the cathode of a vacuum tube? Certainly they are encouraged to do so by the repulsion of the negative charge placed on the cathode and the attraction from the net positive charge of the anode, but these are not strong enough to rip electrons out of atoms by main force `-` if they were, then the entire apparatus would have been instantly vaporized as every atom was simultaneously ripped apart!
The raisin cookie model leads to a simple explanation. We know that heat is the energy of random motion of atoms. The atoms in any object are therefore violently jostling each other all the time, and a few of these collisions are violent enough to knock electrons out of atoms. If this occurs near the surface of a solid object, the electron may can come loose. Ordinarily, however, this loss of electrons is a self-limiting process; the loss of electrons leaves the object with a net positive charge, which attracts the lost sheep home to the fold. (For objects immersed in air rather than vacuum, there will also be a balanced exchange of electrons between the air and the object.)
This interpretation explains the warm and friendly yellow glow of the vacuum tubes in an antique radio. To encourage the emission of electrons from the vacuum tubes' cathodes, the cathodes are intentionally warmed up with little heater coils.
Discussion Questions
A Today many people would define an ion as an atom (or molecule) with missing electrons or extra electrons added on. How would people have defined the word “ion” before the discovery of the electron?
B Since electrically neutral atoms were known to exist, there had to be positively charged subatomic stuff to cancel out the negatively charged electrons in an atom. Based on the state of knowledge immediately after the Millikan and Thomson experiments, was it possible that the positively charged stuff had an unquantized amount of charge? Could it be quantized in units of +e? In units of +2e? In units of +5/7e?
26.3 The electron by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.