5.4 Transmission of forces by low-mass objects by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

5.4 Transmission of forces by low-mass objects

You're walking your dog. The dog wants to go faster than you do, and the leash is taut. Does Newton's third law guarantee that your force on your end of the leash is equal and opposite to the dog's force on its end? If they're not exactly equal, is there any reason why they should be approximately equal?

If there was no leash between you, and you were in direct contact with the dog, then Newton's third law would apply, but Newton's third law cannot relate your force on the leash to the dog's force on the leash, because that would involve three separate objects. Newton's third law only says that your force on the leash is equal and opposite to the leash's force on you,

`F_(yL)= - F_(Ly)`,

and that the dog's force on the leash is equal and opposite to its force on the dog

`F_(dL)= - F_(Ld)`.

Still, we have a strong intuitive expectation that whatever force we make on our end of the leash is transmitted to the dog, and vice-versa. We can analyze the situation by concentrating on the forces that act on the leash, `F_(dL)` and `F_(yL)`. According to Newton's second law, these relate to the leash's mass and acceleration:

`F_(dL)+F_(yL)=m_(L)a_(L)`.

The leash is far less massive then any of the other objects involved, and if `m_L` is very small, then apparently the total force on the leash is also very small, `F_(dL)` + `F_(yL)~~` 0, and therefore

`F_(dL)≈ - F_(yL)`.

Thus even though Newton's third law does not apply directly to these two forces, we can approximate the low-mass leash as if it was not intervening between you and the dog. It's at least approximately as if you and the dog were acting directly on each other, in which case Newton's third law would have applied.

In general, low-mass objects can be treated approximately as if they simply transmitted forces from one object to another. This can be true for strings, ropes, and cords, and also for rigid objects such as rods and sticks.

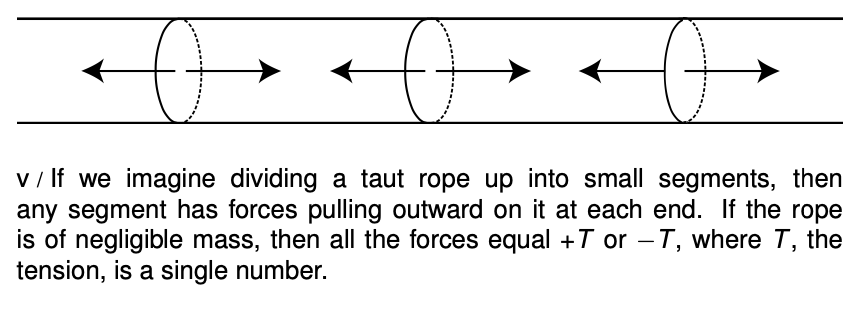
If you look at a piece of string under a magnifying glass as you pull on the ends more and more strongly, you will see the fibers straightening and becoming taut. Different parts of the string are apparently exerting forces on each other. For instance, if we think of the two halves of the string as two objects, then each half is exerting a force on the other half. If we imagine the string as consisting of many small parts, then each segment is transmitting a force to the next segment, and if the string has very little mass, then all the forces are equal in magnitude. We refer to the magnitude of the forces as the tension in the string, `T`.

The term “tension” refers only to internal forces within the string. If the string makes forces on objects at its ends, then those forces are typically normal or frictional forces (example 9).

Example 9: Types of force made by ropes

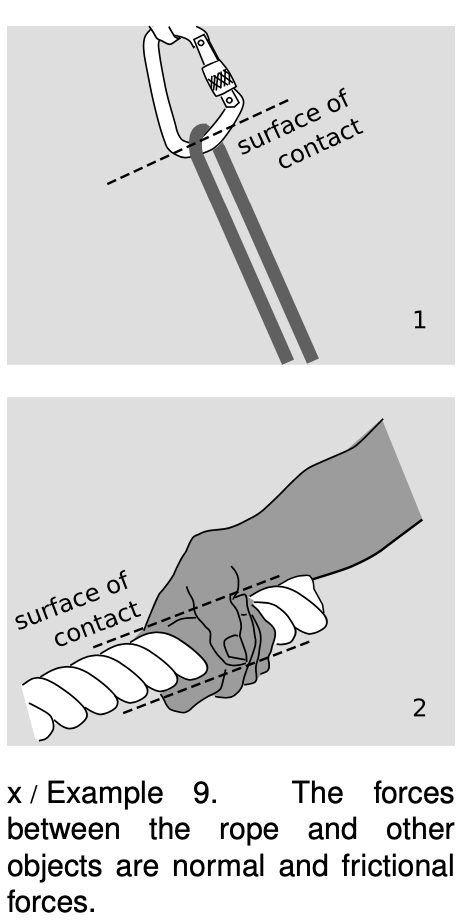
Analyze the forces in figures x/1 and x/2. `=>`

In all cases, a rope can only make “pulling” forces, i.e., forces that are parallel to its own length and that are toward itself, not away from itself. You can't push with a rope! `=>` 

In x/1, the rope passes through a type of hook, called a carabiner, used in rock climbing and mountaineering. Since the rope can only pull along its own length, the direction of its force on the carabiner must be down and to the right. This is perpendicular to the surface of contact, so the force is a normal force.

(There are presumably other forces acting on the carabiner from other hardware above it.)

In figure x/2, the rope can only exert a net force at its end that is parallel to itself and in the pulling direction, so its force on the hand is down and to the left. This is parallel to the surface of contact, so it must be a frictional force. If the rope isn't slipping through the hand, we have static friction. Friction can't exist without normal forces. These forces are perpendicular to the surface of contact. For simplicity, we show only two pairs of these normal forces, as if the hand were a pair of pliers.

force acting on person	force related to it by Newton's third law
rope's static frictional force on person ?	person's static frictional force on rope ?
rope's normal force on person ?	person's normal force on rope ?
rope's normal force on person ?	person's normal force on rope ?

(There are presumably other forces acting on the person as well, such as gravity.)

If a rope goes over a pulley or around some other object, then the tension throughout the rope is approximately equal so long as the pulley has negligible mass and there is not too much friction. A rod or stick can be treated in much the same way as a string, but it is possible to have either compression or tension.

Discussion Question

A   When you step on the gas pedal, is your foot's force being transmitted in the sense of the word used in this section?

5.4 Transmission of forces by low-mass objects by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.