The Terminal Velocity calculator computes the maximum velocity that an object can achieve falling freely through the Earth's atmosphere based on the surface area (A), a drag coefficient (Cd), the density of the air (ρ), the mass of the object (m) and the acceleration due to gravity(g). Common Drag Coefficients 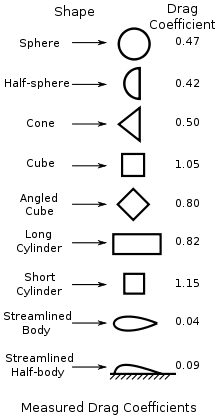
INSTRUCTIONS: Choose units and enter the following:
- (A) Surface area of falling object in the direction of motion.
- (Cd) Drag coefficient
- (ρ) Density of fluid (e.g. air).
- (m) Mass of falling object.
- (g) Acceleration due to gravity.
Terminal Velocity (Vt): The terminal velocity is returned in meters per second (m/s). However, this can be automatically converted to other velocity units via the pull-down menu.
Note: Density of air has a default of 1.2754 kg/m3 (IUPAC standard temperature and pressure (0 C and 100 kPa), dry air). The acceleration due to gravity has a default of 9.80665 m/s2 for the mean acceleration due to gravity on Earth at Sea Level. The user can enter different values and override the defaults by clicking on the input fields and entering different values.
The Math / Science
Terminal velocity is the highest velocity attainable by an object in free fall. It occurs once the sum of the drag force (Fd) and buoyancy equals the downward force of gravity (FG) acting on the object. Since the net force on the object is zero, the object has zero acceleration.
In fluid dynamics, an object is moving at its terminal velocity if its speed is constant due to the restraining force exerted by the fluid through which it is moving.
As the speed of an object increases, the drag force acting on the object, resultant of the substance (e.g., air or water) it is passing through, increases. At some speed, the drag or force of resistance will equal the gravitational pull on the object (buoyancy is considered below). At this point the object ceases to accelerate and continues falling at a constant speed called terminal velocity (also called settling velocity). An object moving downward with greater than terminal velocity (for example because it was thrown downwards or it fell from a thinner part of the atmosphere or it changed shape) will slow down until it reaches terminal velocity. Drag depends on the projected area, and this is why objects with a large projected area relative to mass, such as parachutes, have a lower terminal velocity than objects with a small projected area relative to mass, such as bullets.
The formula for terminal velocity—without considering buoyancy effects—is given by:
`V_t= \sqrt{\frac{2·m·g}{ρ·A·Cd }}`
where:
- Vt is terminal velocity
- m is the mass of the falling object,
- g is the acceleration due to gravity,
- Cd is the drag coefficient,
- ρ is the density of the fluid or gas through which the object is falling, and
- A is the projected area of the object.
In reality, an object approaches its terminal velocity asymptotically.
Examples
Based on wind resistance, for example, the terminal velocity of a skydiver in a belly-to-earth (i.e., face down) free-fall position is about 195 km/h (122 mph or 54 m/s).[2] This velocity is the asymptotic limiting value of the acceleration process, because the effective forces on the body balance each other more and more closely as the terminal velocity is approached. In this example, a speed of 50% of terminal velocity is reached after only about 3 seconds, while it takes 8 seconds to reach 90%, 15 seconds to reach 99% and so on.
Higher speeds can be attained if the skydiver pulls in his or her limbs (see also freeflying). In this case, the terminal velocity increases to about 320 km/h (200 mph or 90 m/s),[2] which is almost the terminal velocity of the peregrine falcon diving down on its prey. The same terminal velocity is reached for a typical .30-06 bullet dropping downwards—when it is returning to earth having been fired upwards, or dropped from a tower—according to a 1920 U.S. Army Ordnance study.[4]
Competition speed skydivers fly in a head-down position and have reached 531 km/h (330 mph). The current absolute record is held by Alan Eustace of Google who jumped from a height of 135,000 feet (41,000 m) and reached 1,322 km/h (821 mph) beating Felix Baumgartner's record.
Physics
Buoyancy effects, due to the upward force on the object by the surrounding fluid, can be taken into account using Archimedes' principle: the mass m has to be reduced by the displaced fluid mass \rho\mathcal{V}, with \mathcal{V} the volume of the object. So instead of m use the reduced mass m_r=m-\rho\mathcal{V} in this and subsequent formulas.
On Earth, the terminal velocity of an object changes due to the properties of the fluid, the mass of the object and its projected cross-sectional surface area.
Air density increases with decreasing altitude, ca. 1% per 80 meters (260 ft) (see barometric formula). For objects falling through the atmosphere, for every 160 metres (520 ft) of falling, the terminal velocity decreases 1%. After reaching the local terminal velocity, while continuing the fall, speed decreases to change with the local terminal velocity.
See Also
- Motion Calculator
- Velocity Calculator
- Vector (3D) Calculator
- Force of Drag Calculator
- Force of Lift Calculator
Reference
- Wikipedia - en.wikipedia.org/wiki/Drag_coefficient
- Wikipedia - en.wikipedia.org/wiki/Terminal_velocity