Bernoulli's Equation is one of the most important/useful equations in fluid mechanics. Many problems relating to real fluid are analyzed with a form of the Bernoulli equation.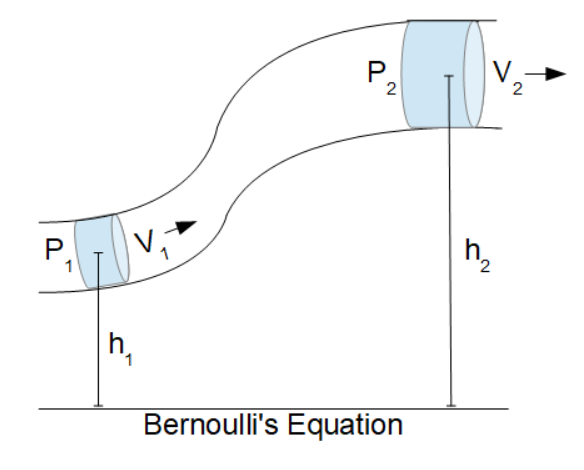 
This calculator has Bernoulli's Equation Solved for:
Based on the continuity equation and conservation of energy where total energy, Potential Energy and Kinetic Energy, are conserved, Bernoulli stated that:
`P + 1/2 rho * V^2 + rho *g*h = C` where: C is a constant.
In a combined system of non-compressible fluids, Bernoulli asserted that the relationship of pressure, density, velocity and elevation can be equated in Bernoulli' Equation:
`P_1 + ½ rho * V_1^2 + rho *g*h_1 = P_2 + ½ rho * V_2^2 + rho *g*h_2`
Bernoulli's Equation solved for Pressure is:
`P_1 = ρ*g [(V_2^2 -V_1^2)/(2*g) + (h_2-h_1) + P_2/(ρ*g)]`
Bernoulli's Equation solved for Velocity is:
`V_1 = sqrt(V_2^2 +2 *g* (h_2-h_1) + 2/rho(P_2 -P_1) )`
Bernoulli's Equation solved for Elevation is:
`h1 = (P_2 - P_1 + ρ*g*h2+1/2*ρ*v2^2-1/2*ρ*v1^2)/(ρ*g)`
where:
- V1 is the velocity at elevation 1
- P1 is the pressure at elevation 1
- h1 is the height of elevation 1
- P2 is the pressure at elevation 2
- V2 is the velocity at elevation 2
- h2 is the height of elevation 2
- ρ is the density of the fluid
- g is the acceleration due to gravity
References
- Young, Hugh and Freeman, Roger. University Physics With Modern Physics. Addison-Wesley, 2008. 12th Edition, (ISBN-13: 978-0321500625 ISBN-10: 0321500628 ) Pg 468, eq 14.17
- Instructional Video by Paul Andersen on Youtube