The Combinatorics Calculator contains standard counting equations that are commonly used in combinatorics including the following:

• `n! ` - factorial
• `n!  sqrt(2 pi n) (n/e)^n ` - Stirling's factorial approximation
• `{::}_nC_k` - combinations
• `C_r(n,k)` - combinations with repetitions
• `{::}_nP_k` - permutations
• `P_r(n)` - permutations with repetitions
• `P_(comp)(n,2)` - Comparison permutations
• `P_c (n,r)` - Circular r-Permutations of n Elements 

factorial

In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. For example,
    `5! = 5 xx 4 xx 3 xx 2 xx 1 = 120`
The value of 0! is 1, according to the convention for an empty product.
The factorial operation is encountered in many areas of mathematics, notably in combinatorics, algebra, and mathematical analysis. Its most basic occurrence is the fact that there are n! ways to arrange n distinct objects into a sequence (i.e., permutations of the set of objects). This fact was known at least as early as the 12th century, to Indian scholars. Fabian Stedman in 1677 described factorials as applied to change ringing. After describing a recursive approach, Stedman gives a statement of a factorial (using the language of the original):
   Now the nature of these methods is such, that the changes on one number comprehends [includes] the changes on all lesser numbers, ... insomuch that a compleat Peal of changes on one number seemeth to be formed by uniting of the compleat Peals on all lesser numbers into one entire body;
The notation n! was introduced by Christian Kramp in 1808.
The definition of the factorial function can also be extended to non-integer arguments, while retaining its most important properties; this involves more advanced mathematics, notably techniques from mathematical analysis. 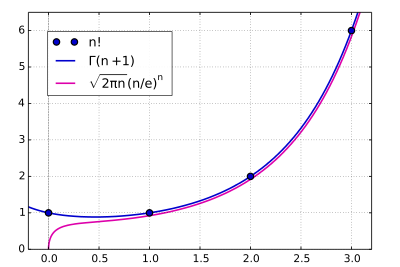Stirling's approximation

Stirling's approximation

Stirling's approximation (or Stirling's formula) is an approximation for factorials. It is a very powerful approximation, leading to accurate results even for small values of n. It is named after James Stirling, though his role in the discovery of the formula makes this attribution an example of Stigler's law of eponymy.
The formula as typically used in applications is
    `ln(n!) = n\ln(n) - n +O(\ln(n))`
(in big O notation). The next term in the O(ln(n)) is `(1/2)ln(2 pi n)`; a more precise variant of the formula is therefore
    `n!  sqrt{2 pi n}(n/e)^n`

Combination

In mathematics, a combination is a way of selecting items from a collection, such that (unlike permutations) the order of selection does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. If the set has n elements, the number of k-combinations is equal to the binomial coefficient

    `((n),(k)) =  (n(n-1)...(n-k+1))/(k(k-1)...1)`,

which can be written using factorials as `frac{n!}{k!(n-k)!}` whenever `k leq n`, and which is zero when `k gt n`. The set of all k-combinations of a set S is sometimes denoted by `((S),(k))`.

Combinations refer to the combination of n things taken k at a time without repetition. To refer to combinations in which repetition is allowed, the terms k-selection, k-multiset, or k-combination with repetition are often used. If, in the above example, it was possible to have two of any one kind of fruit there would be 3 more 2-selections: one with two apples, one with two oranges, and one with two pears.

Although the set of three fruits was small enough to write a complete list of combinations, with large sets this becomes impractical. For example, a poker hand can be described as a 5-combination (k = 5) of cards from a 52 card deck (n = 52). The 5 cards of the hand are all distinct, and the order of cards in the hand does not matter. There are 2,598,960 such combinations, and the chance of drawing any one hand at random is 1 / 2,598,960.

Combinations with Repetitions

A k-combination with repetitions, or k-multicombination, or multisubset of size k from a set S is given by a sequence of k not necessarily distinct elements of S, where order is not taken into account: two sequences of which one can be obtained from the other by permuting the terms define the same multiset. In other words, the number of ways to sample k elements from a set of n elements allowing for duplicates (i.e., with replacement) but disregarding different orderings (e.g. {2,1,2} = {1,2,2}). Associate an index to each element of S and think of the elements of S as types of objects, then we can let x_i denote the number of elements of type i in a multisubset. The number of multisubsets of size k is then the number of nonnegative integer solutions of the Diophantine equation:

    `x_1 + x_2 + \ldots + x_n = k`. 

Permutations

The notion of permutation relates to the act of rearranging,or permuting, all the members of a set into some sequence or order (unlike combinations, which are selections of some members of the set where order is disregarded). For example, written as tuples, there are six permutations of the set {1,2,3}, namely: (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), and (3,2,1). As another example, an anagram of a word, all of whose letters are different, is a permutation of its letters. The study of permutations of finite sets is a topic in the field of combinatorics.

Permutations occur, in more or less prominent ways, in almost every area of mathematics. They often arise when different orderings on certain finite sets are considered, possibly only because one wants to ignore such orderings and needs to know how many configurations are thus identified. For similar reasons permutations arise in the study of sorting algorithms in computer science.

The number of permutations of n distinct objects is n factorial usually written as n!, which means the product of all positive integers less than or equal to n.

In algebra and particularly in group theory, a permutation of a set S is defined as a bijection from S to itself. That is, it is a function from S to S for which every element occurs exactly once as an image value. This is related to the rearrangement of the elements of S in which each element s is replaced by the corresponding f(s). The collection of such permutations form a group called the symmetric group of S. The key to this group's structure is the fact that the composition of two permutations (performing two given rearrangements in succession) results in another rearrangement. Permutations may act on structured objects by rearranging their components, or by certain replacements (substitutions) of symbols.

In elementary combinatorics, the k-permutations, or partial permutations, are the ordered arrangements of k distinct elements selected from a set. When k is equal to the size of the set, these are the permutations of the set.

Permutations with Repetitions

Ordered arrangements of the elements of a set S of length n where repetition is allowed are called n-tuples, but have sometimes been referred to as permutations with repetition although they are not permutations in general. They are also called words over the alphabet S in some contexts. If the set S has k elements, the number of n-tuples over S is:    `k^n`.

There is no restriction on how often an element can appear in an n-tuple, but if restrictions are placed on how often an element can appear, this formula is no longer valid.

References

• wikipedia - en.wikipedia.org/wiki/Factorial
• wikipedia - en.wikipedia.org/wiki/Stirling%27s_approximation
• wikipedia - en.wikipedia.org/wiki/Combination