Cylinder - Height from Surface Area

The Height of a Cylinder from Surface Area calculator computes the height of a cylinder based on the total surface area of a cylinder including its ends and the radius.Right Cylinder

Cylinder Height from the Surface Area

1. Choose units
2. Enter the radius (r) of the cylinder.
3. Enter the surface area (SA) of the cylinder.

Cylinder Height (h): The calculator returns the height (h) meters.  However, this can be automatically converted to other length units via the pull-down menu.

Related Cylinder Calculator Functions:

1. Compute the Lateral Surface Area (sides) of the cylinder based on height and radius.
2. Compute the Total Surface Area of a cylinder including the sides, top and bottom.
3. Compute the Volume of a cylinder based on cylinder height and radius
4. Compute the Height of a cylinder based on the volume and radius.
5. Compute the Radius of a cylinder based on the volume and height.
6. Compute the Mass or Weight of a cylinder as a function of the volume and mean density of the substance of the cylinder.  
7. Compute the Density of a cylinder.
8. Compute the Lateral Surface Area of a Slanted cylinder.
9. Compute the Volume of a Slanted cylinder.
10. Compute the Weight or Mass of a Slanted cylinder.
11. Compute the moment of inertia of a cylinder shaped object based around the central axis
12. Compute the moment of inertia of a  cylinder shaped object around the end of the cylinder
13. Compute the moment of inertia of a  cylinder shaped object perpendicular to the central axis.
14. Look up the mean density of common substances (useful in calculating the mass/weight and the moments of inertia)

The Math

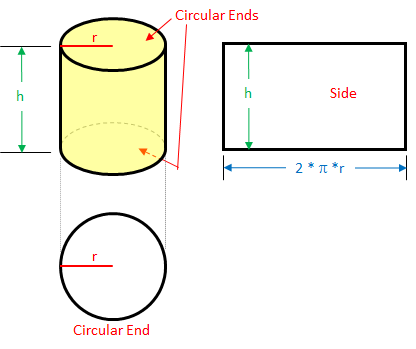We can envision the cylinder as having three separate surfaces:

• the circular top (visible in the picture), where A = ?•r²
• the circular bottom (hidden in the picture's perspective), where A = ?•r²
• the rectangle lateral surface (imagine the sides of the cylinder rolled out flat), where where A = 2•?•r•h

And thus the surface area can be represented simply as:

     [1] `"Surface Area"_"(Cylinder)" = "Area"_"(Side)" + 2 * "Area"_"(Circular End)"`

We can compute the area of the circle on each of the two circular cylinder ends using the well remembered formula for a circle's area:

     [2]   A = ?•r²

We not that the length of the side unwrapped is equivalent to the circle's circumference, and we know the circle's circumference is given by:

     [3] C = 2 • ? • r

Then the area of the side of the cylinder has height h its area can be computed as:

     [4] `"Area"_"(Side)" = "Height" * "Width" = h * "circumference" = h * 2 * pi * r`

Then substituting [2] and [4] into [1] we get:

     [5] `"Surface Area"_"(Cylinder)" = h * 2 * pi * r + 2 * (pi * r^2)`

The formula for the height (h) of a cylinder based on the Surface Area and the Radius is:

`h = \frac{A - (2\pir^2)}{2\pir)`

where:

• h is the height or length of the cylinder
• A is the surface area of the cylinder
• r is the radius of the cylinder