Pyramid - Volume

The Volume of a Pyramid calculator 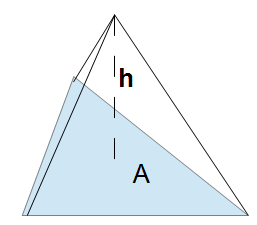 computes the volume based on the area of the base and the height.

INSTRUCTIONS: Choose units and enter the following:

• (A) Area of the Base
• (h) Height

Pyramid Volume (V): The calculator returns the volume in cubic meters.  However this can be automatically converted to compatible units via the pull-down menu.

The Math / Science

The formula for the volume of a pyramid is:

      `V = 1/3 * A * h`

where:

• V = Volume of Pyramid
• A = Area of the base
• h = height

Pyramid Calculators

• Pyramid Geometries
• Volume of a Pyramid
• Mass or Weight of a Pyramid 
• Volume of a Frustum of a Pyramid
• Mass of a Frustum of a Pyramid
• Volume of a Polygon Based Pyramid
• Mass of a Polygon Based Pyramid
• Volume of a Frustum of a Polygon Based Pyramid
• Mass of a Frustum of a Polygon Based Pyramid

A regular pyramid is a type of pyramid that has the following characteristics:

1. Base: The base of a regular pyramid is a regular polygon, meaning all sides of the polygon are equal in length, and all interior angles are equal. Examples of regular polygons include equilateral triangles, squares, and regular pentagons.
2. Apex: The apex is the point directly above the center of the base. In a regular pyramid, the apex is aligned such that the line segment (height) from the apex to the center of the base is perpendicular to the base.
3. Lateral Faces: The lateral faces of the pyramid are congruent isosceles triangles. Each triangle shares a side with the base of the pyramid and meets at the apex.
4. Height: The height of the pyramid is the perpendicular distance from the apex to the center of the base.

Because of these properties, a regular pyramid is symmetric around its vertical axis (the line connecting the apex to the center of the base).