The Square Root of Complex Numbers calculator generates the principal square root of the two square roots of a complex number.
INSTRUCTIONS: Enter the following:
- (x) Real Part
- (y) Imaginary Part
Square Root of Complex Numbers (`sqrt(x+iy)`): The calculator returns the square root.
The Math / Science
The formula for the square root of a complex number is:
`sqrt(x+iy) = (sqrt(x^2 + y^2))^(1/4)[cos(("atan"(x/y))/2 ) + i sin(("atan"(x/y))/2 )]`
where:
- x = real part
- y = imaginary part
Author: GerryPerham, also known as Gerrad Param, Knowledge Wraith of the Boran Empire.
See Also
The Quaternion Calculator includes functions associated with quaternion mathematics. These include the following:
- Quaternion Addition
- Quaternion Subtraction
- Quaternion Multiplication
- Quaternion Magnitude
- Quaternion Versor
- Quaternion Conjugate
- Quaternion Inverse
- Quaternion of Rotation
- Vector Rotation
Quaternions
Quaternions can be represented in several ways. One of the ways is similar to the way complex
numbers are represented:
q ≡ q4 + q1i + q2j + q3k,
in which q1 , q2 , q3 and q4 , are real numbers, and i, j, and k, are unit “vectors” which obey similar rules to the vectors of the same names found in vector analysis, but with an additional similarity to the i of complex arithmetic which equals `sqrt(-1)` . The multiplication rules for i , j , and k are depicted
conceptually as follows:
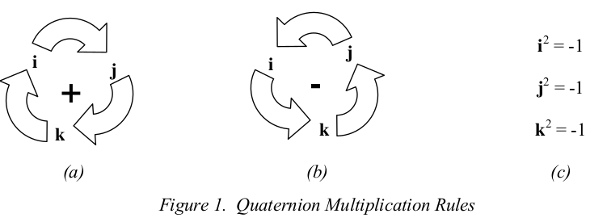
That is, i j = + k, j k = + i, etc. , from figure 1(a) , and j i = - k, i k = -j , etc., from figure 1(b) . Expressed
in this form, the multiplication rules are very easy to remember. Note that the cross products of i, j , and
k obey the rules of vector cross product multiplication, where, for example, given the orthogonal axes,
x, y, and z: x × y = z, y × z = x , and z × x = y .
Note: Quaternions are not commutative, and the following should be noted:
q1*q2 ? q2 * q1
q1*q2 ? -q2 * q1, but
(q1 * q2) * q3 = q1 * (q2 * q3)