The Area of an Arc Segment of a Circle formula, A = ½• r²• (θ - sin(θ)), computes the area defined by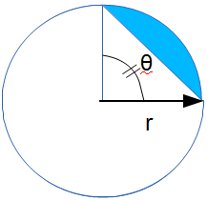
A = f(r,θ)
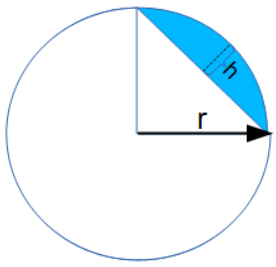A = f(r,h) an arc and the chord connecting the ends of the arc (see blue area of diagram).
INSTRUCTIONS: Choose units and enter the following:
- (r) - This is the radius of the circle.
- (θ) - This is the angle defining the arc.
Area of an Arc Segment of a Circle (A): The calculator returns the area (A) in square meters. However the user can automatically convert the output units to numerous other compatible units via the pull-down menu.
Related Calculators
The Math / Science
If θ is unknown, the same area can be calculated if the depth (h) from the edge of the circle toward the center is known. (See figure) The following equation calculates the area using r and h: (Click on formula for solver)
`A=1/2 * r^2 * (2 cos^-1((r-h)/r)- sin(2 cos^-1((r-h)/r))`
CIRCLE PARTS 
For the area of different parts or segments of a circle, the following calculators will help. The calculator returns the area in square meters. However this can be automatically converted to other area units such as square feet or acres via the pull-down menu:
- Area based on radius:: A =`pi r^2`
- Area based on diameter: A = `pi (d/2)^2`
- Area based on circumference: A = `pi (c/(2pi))^2`
- Area of a Sector (wedge, pie piece) based on radius (r) and angle (`theta`)
- Area of Arc Segment given the radius (r) and angle (`theta`)
- Area of Arc Segment given radius (r) and the depth (h) into the circle
- Area of Circle Incribed within a triangle given three sides (a,b,c) of the triangle
- Area of Cirlce Circumscribing a triangle given three sides (a,b,c) of the triangle
- Area of Annulus given the inner radius (r) and outer radius (R)
Notes
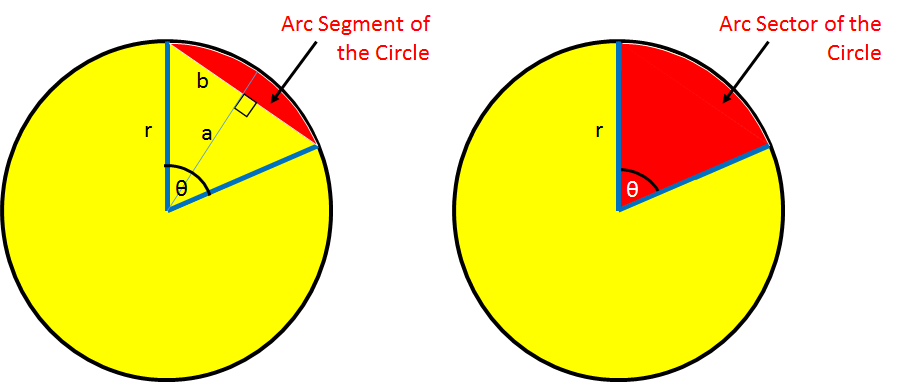
The area described in red in the first image on the left below is the area of the arc segment of of a circle. The area of the arc segment is defined by the angle `theta` and the circle's radius, r.
To find the area of the arc segment, we first find the area of the arc sector, shown in red in the second image on the right. This equations area is derived in the equation, "Circle -area of sector"
The simplified form of the formula for the area of the sector depends on whether the units used are degrees or radians.
)))
|
The area of the segment can be seen graphically to be the difference between the area of the sector (defined by r and `theta` in the equation above) and the the area of the triangle defined by r and `theta` above -- or more properly the summation of the area of the two right triangles with sides r, a, and b in the left picture. Thus the area of one of the combined triangle whose center angle is `theta` is defined as 2 * 1/2 * base * 1/2 * height. `"Area"_"triangle"` = 2 * (1/2 * base * height) = 2 * 1/2 * (r * sin(`theta`/2)) * (r * cos(`theta`/2)) = `r^2` * sin(`theta`/2) * cos(`theta`/2) Using the trigonometric identity sin(2u) = 2 sin(u) * cos(u) `=>` sin(u) * cos(u) = sin(2U)/2 we see sin(`theta`/2) * cos(`theta`/2) = `sin(theta)/2` So, `"Area"_"triangle"` = `r^2` * `sin(theta)/2` Then `"Area"_"segment"` = `"Area"_"sector" - "Area"_"triangle"` where from the derivation of the area of a circle sector we have:
So, for units given in radians, we have the \
|