`det = |A|`

Enter a value for all fields

The Determinant of a 3x3 Matrix calculator compute the determinant of a 3x3 matrix.

INSTRUCTIONS: Enter the following:

• (A) 3x3 Matrix

Determinant (det): The calculator returns the determinate as a real number.

The Math / Science

The Determinant of a 3x3 calculator computes the determinant of a 3x3 matrix, a useful mathematical construct derived from a square matrix:

A = `|[A_11,A_12,A_13],[A_21,A_22,A_23],[A_31,A_32,A_33]|`

The determinant can be used for a number of linear algebra applications like solving a set of linear equations and determining the characteristic polynomial of a matrix in computing eigenvalues.

INPUTS

Inputs to the matrix above are nine numeric values, where the cells of the matrix are ordered as:

A₁₁, A₁₂, A₁₃
A₂₁, A₂₂, A₂₃
A₃₁, A₃₂, A₃₃

OUTPUT

Output for the formula is the determinant of matrix A, illustrated by the following graphic:
              

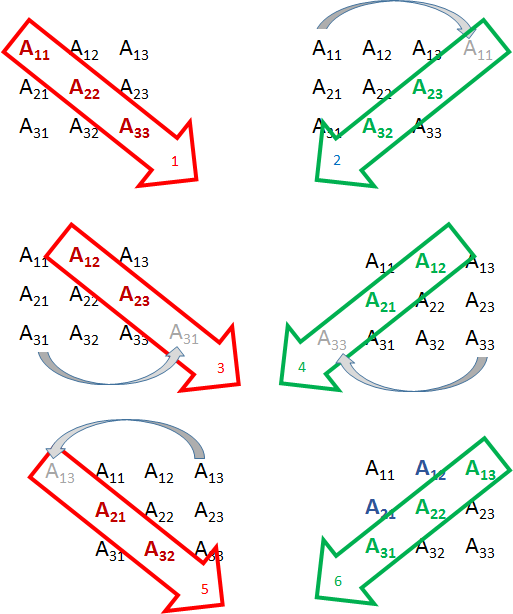
COMPUTING THE DETERMINANT

Six Terms

The picture above shows the order of the multiplications to obtain six terms which are then added together to compute the determinant. The picture gives you a visual pattern to employ when computing a determinant.

Note that four of the six diagonals intersect a term which has to be brought over to complete the diagonal.  Another way to think about it visually, is that the diagonal for Term 3, which starts with `A_12` wraps around the matrix to hit `A_31`.

The Product That Is The First Term

To compute the first term you multiply the terms on the red diagonal:  Term 1 = `A_11 * A_22 * A_33`

The Six Terms Are Also Products

Let's look at how the six terms are obtained. 

Each of six terms then compute like:

• Term 1 = `A_11 * A_22 * A_33`
• Term 2 = `A_11 * A_23 * A_32`
• Term 3 = `A_12 * A_23 * A_31`
• Term 4 = `A_12 * A_21 * A_33`
• Term 5 = `A_13 * A_21 * A_32`
• Term 6 = `A_13 * A_22 * A_31`

Sum The Terms To Finish the Determinant

det(A) = (Term 1 - Term2) + (Term 3 - Term 4) + (Term 5 - Term 6)

---

Matrix Calculators

• Determinant of 3-by-3 Matrix
• Characteristic Polynomial of a 3x3 matrix
• Inverse of a 3x3 Matrix
• Transpose of a 3x3 Matrix
• Trace of a 3x3 Matrix
• Mirror of a 3x3 Matrix
• 3x3 Matrix Characteristics (Trace, Determinant, Inverse, Characteristic Polynomial)
• Product of a 3x3 matrix and a Scalar
• Product of a 3x3 matrix and a 3x1 matrix
• Product of two 3x3 matrices
• Solving 3 Equations with 3 Unknowns
• Cramer's Rule (three equations, solved for x, y and z)
• Cramer's Rule Calculator