Vector Sum of Forces (2D)
Tags | |
UUID | 0bf3c046-cde4-11e4-a3bb-bc764e2038f2 |
The Vector Sum of Forces (2D) calculator computes the sum of two vectors by summing the x and y components of the two vectors.
INSTRUCTIONS: Choose units and enter the following:
- (`vecF_"ax"`) x component of vector A
- (`vecF_"ay"`) y component of vector A
- (`vecF_"bx"`) x component of vector B
- (`vecF_"by"`) y component of vector B
Vector Sum of Forces (2D) (`vecF_"net"`): The resulting vector is returned in Newtons.
The Math / Science
The Vector Sum of Forces (2D) equation computes the sum of two vectors by summing the x and y components of the two vectors.
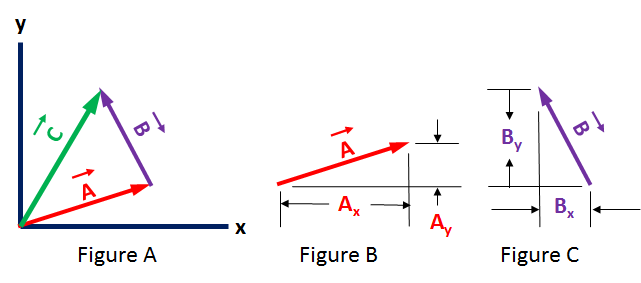
To simplify the graphical example we show vector `vecA` begins at the origin of the Cartesian axes and so that vector `vecA` points to the point [`vecA_x`, `vecA_y`]. Nevertheless, we know that these vectors and this vector addition can occur anywhere on the X/Y plane.
Notes
A vector is a mathematical concept of an object that has direction and length. A line alone is not a vector but a line with orientation spanning the distance between two points in space is a vector.
Figure A shows the vector summation: `vecC` = `vecA` + `vecB` with `vecA` having it's start at the origin for simplification.
Figure B shows the x and y components of vector `vecA` (in red).
Figure C shows the x and y components of vector `vecB` (in purple).
Vector `vecC`'s coordinates = [`vecC_x` , `vec C_y`] = [`vec A_x` + `vecB_x`, `vecA_y` + `vecB_y`]
- Comments
- Attachments
- Stats
No comments |
