The Motion and Travel calculator 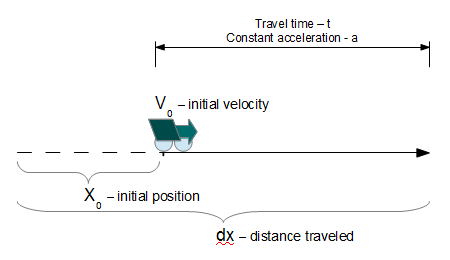Constant Acceleration Motioncontains equations for physical motion on the earth, in the air and in space.

Description

The Motion and Travel calculator has physics equations related to measurements, distances and other factors associated with motion on the earth and in space.  It includes the ability to calculate distances traveled, time required to cross those distances based on user entered velocities.  The equations are general (kinematic) physics equations, astronomy/astrodynamics equations and Euclidean geometry equations.  The astronomical equations include distance data to the moon, planets, sun, stars and galaxies.  The information is reasonably accurate and includes some fun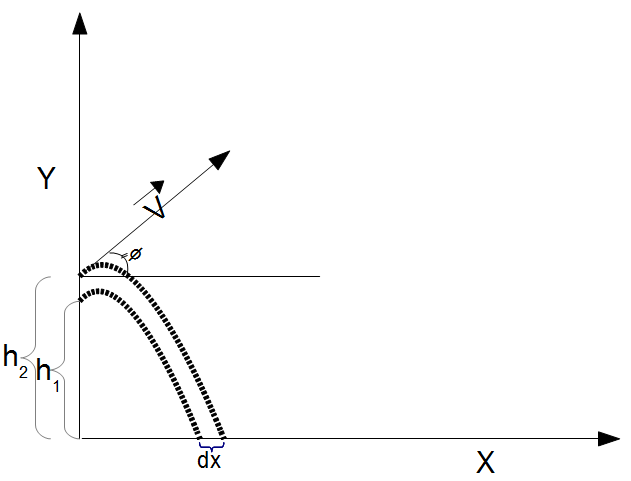  Ballistic Range and change based on delta heightconcepts from science fiction including Star Trek's warp speed in some of the astronomical calculations.

The equations include the following:

• Distance: This is the distance traveled based on initial position, initial velocity, constant acceleration and time of travel.
• Ballistic Range: This is the distance traveled by an object in free flight based on a launch angle, height above the plane and an initial velocity.
• Ballistic Travel Time:  This is the time of flight for ballistic (free flight) object.
• Max Ballistic Height: This is the maximum height above the plane achieved by a ballistic (free flight) object. 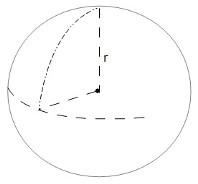Great circle arc travel 
• Ballistic Range - Delta Height: This is the change in range of a ballistic flight based on the change in height of the launch point.
• Earth - Distance: This is the distance in a create circle arc between to points on the earth.
• Earth - Travel Time: This is the time required to travel between two points on the earth at a constant velocity.
• Astro Distances:  This is the linear distance between the Earth and other objects in the solar system, galaxy and universe at their closest approach.
• Astro Travel Time:  This is Planets in the Solar Systemthe time required to travel between the Earth and other objects in space at specific constant velocities (real and fictional).

Notes

Thanks to my friend Bob Hicks for pointing me to the first Earth distance equations (Haversine)