Force of Sun's gravity on planets
The Force of Sun's Gravity on Planets calculator uses the force of gravity equation to compute the gravitational force between the sun and your selection of a planet.
INSTRUCTIONS:
- Choose a planet from the pull-down list
Force of the Sun's Gravity (F): The calculator returns the force in newtons.
The Math/Science
The Force of Gravity equation computes the gravitational force between the two masses: the Sun and the planet or other body from our solar system. In this equation, the masses are treated as point masses separated by a specified distance.
The Universal Gravitational Constant is 6.67384E-11 m3 / kg * sec2. 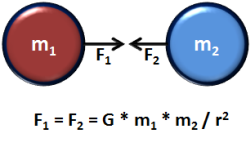 Force of Gravity
Force of Gravity
Newton's law of universal gravitation states that any two bodies in the universe attract each other with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. (Separately it was shown that large spherically symmetrical masses attract and are attracted as if all their mass were concentrated at their centers.) This is a general physical law derived from empirical observations by what Isaac Newton called induction. It is a part of classical mechanics and was formulated in Newton's work Philosophiæ Naturalis Principia Mathematica ("the Principia"), first published on 5 July 1687. (When Newton's book was presented in 1686 to the Royal Society, Robert Hooke made a claim that Newton had obtained the inverse square law from him) In modern language, the law states the following:
|
where:
|
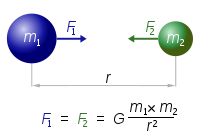 |
Assuming SI units, F is measured in newtons (N), the mass of the Sun and a planet in kilograms (kg), r in meters (m), and the constant G is approximately equal to 6.674×10−11 N m2 kg−2. However, vCalc enables the user enter units in any of the applicable mass units (see pull-down list). The value of the constant G was first accurately determined from the results of the Cavendish experiment conducted by the British scientist Henry Cavendish in 1798, although Cavendish did not himself calculate a numerical value for G. This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force.
Newton's law of gravitation resembles Coulomb's law of electrical forces, which is used to calculate the magnitude of electrical force between two charged bodies. Both are inverse-square laws, in which force is inversely proportional to the square of the distance between the bodies. Coulomb's law has the product of two charges in place of the product of the masses, and the electrostatic constant in place of the gravitational constant.
Newton's law has since been superseded by Einstein's theory of general relativity, but it continues to be used as an excellent approximation of the effects of gravity. Relativity is required only when there is a need for extreme precision, or when dealing with very strong gravitational fields, such as those found near extremely massive and dense objects, or at very close distances (such as Mercury's orbit around the sun).
Newton's theory of gravitation
Main article: Newton's law of universal gravitation  Sir Isaac Newton, an English physicist who lived from 1642 to 1727
Sir Isaac Newton, an English physicist who lived from 1642 to 1727
In 1687, English mathematician Sir Isaac Newton published Principia, which hypothesizes the inverse-square law of universal gravitation. In his own words, "I deduced that the forces which keep the planets in their orbs must [be] reciprocally as the squares of their distances from the centers about which they revolve: and thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the Earth; and found them answer pretty nearly."[3]
Newton's theory enjoyed its greatest success when it was used to predict the existence of Neptune based on motions of Uranus that could not be accounted for by the actions of the other planets. Calculations by both John Couch Adams and Urbain Le Verrier predicted the general position of the planet, and Le Verrier's calculations are what led Johann Gottfried Galle to the discovery of Neptune.
A discrepancy in Mercury's orbit pointed out flaws in Newton's theory. By the end of the 19th century, it was known that its orbit showed slight perturbations that could not be accounted for entirely under Newton's theory, but all searches for another perturbing body (such as a planet orbiting the Sun even closer than Mercury) had been fruitless. The issue was resolved in 1915 by Albert Einstein's new theory of general relativity, which accounted for the small discrepancy in Mercury's orbit.
Although Newton's theory has been superseded, most modern non-relativistic gravitational calculations are still made using Newton's theory because it is a much simpler theory to work with than general relativity, and gives sufficiently accurate results for most applications involving sufficiently small masses, speeds and energies.
Astronomical Units
Because of the enormity of space and the size of the objects studied, the field of astronomy employs units not commonly used in everyday life. Nonetheless, these units do translate into common units at a grand scale, and vCalc provides automatic conversions between units for calculator inputs and answers via the pull-down menus. The following is a brief description on the distance, mass and time units employed in the field of astronomy
Astronomy Distance Units
Astronomical Unit (au): Within our solar system, a common measure of distance is au, which stands for astronomical units. A single astronomical unit is the mean distance from the Sun's center to the center of the Earth.
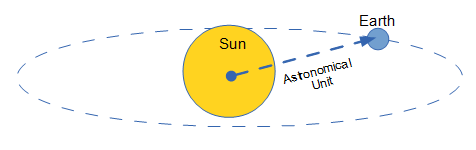
| Astronomical Unit (au) | Distance from Sun (au) |
|---|---|
|
|
Light Travel in Time: Light is a primary observable when studying celestial bodies. For this reason, the distance to these objects are measured in the amount of time it would take light to travel from there to the Earth. We can say that an object is one light-year away, and that means that the object is at a distance where it took an entire year for light from the object to travel to Earth. Since the speed of light is 299,792,458.0 meters per second, one can compute the distance equal to a light year as follows:
1 light year = 299,792,458.0 (meters / second) x 31,536,000 (seconds / year) = 9,460,528,405,000,000 meters
The same exercise can be used for light traveling shorter periods of times, light seconds, light minutes, light hours and light days. Since even these units are not enough when computing distances across the universe, there is also a light relative distance of kilo-light years (1000 light years), or the distance light travels in a thousand years!
| Light Second | Light Minute | Light Hour | Light Day | Light Year | Kilo-Light Year |
|---|---|---|---|---|---|
|
299,786 km 186,278 miles 0.002 au |
17,987,163 km 11,176,705 miles 0.12023 au |
1,079,229,797 km 670,602,305 miles 7.214 au |
25,901,515,140 km 16,094,455,343 miles 173.14 au |
9,460,528,405,000 km 5,878,499,814,210 miles 63,240 au 0.306 parsecs |
9,460,528,405,000,000 km 5,878,499,814,210,000 miles 63,240,000 au 306 parsecs |
Angle Shift Seen from Earth: Because the Earth goes around the Sun, our observation of distant objects such as stars results in an angular shift when observed at opposite sides of the elliptical orbit. This shift is used as the basis of a unit knows as a parsec. A parsec was traditionally defined as the distance where one astronomical unit subtends an angle of one arcsecond. A parsec was redefined in 2015 to 648000/π astronomical units. Proxima Centauri, is the nearest star to the Sun and is approximately 1.3 parsecs (4.2 light-years) from the Sun. A mega-parsec is a million parsecs.
| Parsec | Mega-parsec |
|---|---|
|
|
Astronomy Mass Units
Astronomical units also apply to the mass of enormous objects such as moons, planets and stars. For this reason, astronomy also employs mass units that compare other objects to ones familiar to us. For example, stars are often measured in mass units of solar masses. This is a comparison of their mass to the mass of our sun (one solar_mass). For planets, astronomers use Earth masses and Jupiter masses for understanding the relative size of rocky planets and gas giants.
| Earth Masses | Jupiter Masses | Solar Masses |
|---|---|---|
|
|
|
Astronomy Time Units
Astronomers use the same time units as everyone else, from the very small nanoseconds, to seconds, minutes, hours, days and years. This is true with two exceptions known as sidereal days and sidereal years. These refer to time relative to the celestial objects (the fixed stars). The Earth rotates every 24 hours relative to the Sun. But we are moving in a circle around the Sun. In comparison, the Earth rotates every 23 hours, 56 minutes and 4.0905 seconds (23.9344696 hours) compared to the stars in the celestial sphere. This is known as a sidereal day.
In the same vein, a sidereal year is the time it takes the Earth to complete one orbit around the Sun relative to the celestial sphere. Where a year is 365 days, a sidereal year is 365.256363004 days, or 1,224.5 seconds more than a calendar year.
| Sidereal Day | Sidereal Year |
|---|---|
|
|
Reference
- http://en.wikipedia.org/wiki/Gravitation
- http://en.wikipedia.org/wiki/Newton%27s_law_of_universal_gravitation
Equations and Data Items
Equations and Data Items
- Comments
- Attachments
- Stats
No comments |

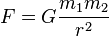 ,
,