The Restoring Torque on a Physical Pendulum calculator computes the restoring torque (τ_z) on a physical pendulum 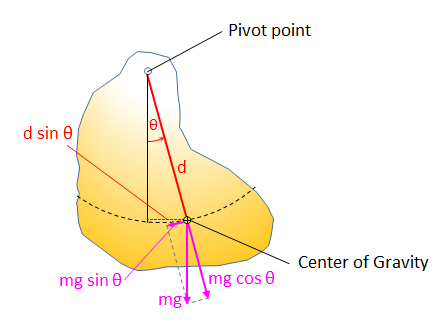based on the mass (m), acceleration due to gravity (g), distance to the center of gravity (d) and the displacement angle (θ).

INSTRUCTIONS: Choose units and enter the following:

• (m) Mass 
• (d) Distance from Pivot Point to Center of Gravity
• (θ) Angle of Displacement

Restoring Torque (τ_z): The calculator returns the torque in Newton Meters (N·m).  However, this can be automatically converted to compatible units (e.g. Joules) via the pull-down menu.  Note, this calculator uses the constant acceleration due to gravity at sea level.

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force combined with the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum, and also to a slight degree on the amplitude, the width of the pendulum's swing.

Types of Pendulums:

• Simple Pendulum – A single mass (bob) attached to a string or rod that swings back and forth.
• Compound Pendulum – A rigid body swinging about a pivot point.
• Foucault Pendulum – Demonstrates the Earth's rotation by slowly changing its plane of motion.
• Torsional Pendulum – Rotates around its axis instead of swinging back and forth.

Applications of Pendulums:

• Used in clocks (grandfather clocks) to regulate time.
• Scientific experiments (measuring gravity).
• Seismometers to detect earthquakes.
• Amusement park rides.

The Pendulum Calculator includes the basic physics formulas and constants for the properties of a pendulum.  These include the following:

• Pendulum Frequency: Computes the frequency (ƒ) of a simple pendulum based on the length (L) of the pendulum.
• Period of a Pendulum: Computes the period (T) of a simple pendulum based on the length (L) of the pendulum arm and the acceleration due to gravity (g).
• Pendulum Length: Computes the length (L) of a simple pendulum based on the period (T) of the pendulum arm and the acceleration due to gravity (g).
• Pendulum Angular Frequency: Computes the angular frequency of a simple pendulum with a small amplitude.
• Angular Frequency of a Physical Pendulum: Computes the approximate value of the angular frequency given that the amplitude of the pendulum is small based on the mass, distance from pivot point to center of mass and the moment of inertia.
• Restoring Torque to a Pendulum: Computes the restoring torque (τz) on a physical pendulum based on the mass (m), acceleration due to gravity (g), distance to the center of gravity (d) and the displacement angle (θ).
• Restoring Force on a Pendulum: Approximates the restoring force on a pendulum based on the mass, length of pendulum and length of arc. 
• Rotational Acceleration of a Physical Pendulum: Approximates the rotational acceleration of a physical pendulum based on the mass (m), acceleration due to gravity (g), distance to the center of gravity (d), impulse (I) and the angle (Θ)
• (g) acceleration due to gravity 

References

Young, Hugh and Freeman, Roger.  University Physics With Modern Physics.  Addison-Wesley, 2008. 12th Edition, (ISBN-13: 978-0321500625 ISBN-10: 0321500628 ) Pg 438, eq 13.36