Lagrange Points L1 and L2
Tags | |
UUID | 240da7cf-569f-11ec-993a-bc764e203090 |
The Lagrange Points (L1 and L2) calculator computes the approximate radius (r) from a smaller mass (M2) to the first two Lagrange Points.
INSTRUCTIONS: Choose units and enter the following:
- (M1) Mass of Larger Object
- (M2) Mass of Smaller Object
- (R) Distance between Objects
Lagrange Point Radii (r): The calculator returns the radii for L1 and L2 in astronomical units (au). However, these can be automatically converted to compatible units via the pull-down menu.
The Math / Science
Lagrangian points, also known as Lagrange points or libration points, are specific positions in space where the gravitational forces of two large bodies, such as a planet and a moon or a planet and the Sun, balance the centrifugal force felt by a smaller object, like a satellite or spacecraft. These points are named after the French mathematician Joseph-Louis Lagrange, who studied them in the 18th century.
There are five Lagrange points labeled L1 through L5. Here's a brief overview of each:
- L1 (Lagrange Point 1): Located along the line connecting the two large bodies and closer to the smaller mass, L1 is a point where the gravitational forces of the two large bodies balance the centrifugal force felt by the smaller object. It is often used for solar observatories, such as the SOHO (Solar and Heliospheric Observatory).
- L2 (Lagrange Point 2): Also situated along the line connecting the two large bodies but on the opposite side from the smaller mass, L2 is another point where gravitational and centrifugal forces are balanced. L2 is utilized for the James Webb Space Telescope (see below).
- L3 (Lagrange Point 3): Located opposite to L1 along the line connecting the two large bodies but farther away from the smaller mass, L3 is theoretically a Lagrange point, but it is unstable. No significant natural objects, like satellites, are located at L3.
- L4 and L5 (Lagrange Points 4 and 5): These points form equilateral triangles with the two large masses. L4 leads the smaller mass in its orbit, and L5 follows it. These points are stable and are often used by natural satellites, such as asteroids, in certain orbital configurations. They are sometimes referred to as Trojan points.
Lagrangian points provide stable locations in space where objects can maintain a relatively constant position relative to the two larger masses. These points have practical applications in space exploration, satellite deployment, and the study of celestial bodies.
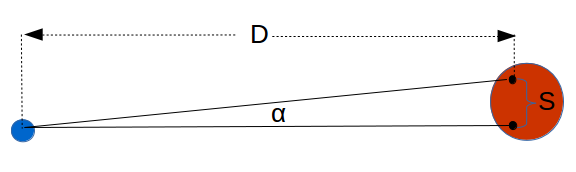
Lagrange Point L1 is located on a line between the two masses where the gravitational force of the two masses are equal. This has the net effect of keeping the object at a constant distance from the two objects. The orbital period of the object is equal to that of the smaller mass object. Normally, a body closer to the larger mass would have a shorter orbital period. However the pull of the smaller object (M2) keeps the object in same rate of rotation around the major object (M1). Lagrange Point L2 is also on the line connecting M1 and M2, but is further from M2 (see diagram). L2 will is the location of the James Web Space Telescope (JWST).
The formula for the radius of Lagrange Points L1 and L2 to M2 is:
r
where:
- r is the distance from the smaller object to the Lagrange point.
- R is the distance between the two major objects
- M1 is the mass of the primary object
- M2 is the mass of the secondary object.
Note: the radius for L1 is the same for L2.
Sun, Earth and Moon Data
- Sun
- Mass of the Sun
- 1 Solar Mass
- 1047.708 Jupiter Masses
- 332,968 Earth Masses
- 1.98855 x 1030 kilograms
- Mass of the Sun
- Earth
- Mass of the Earth: 5.97219E24 kg
- Earth Aphelion: 1.01558932154734 au
- Mean Distance to Sun: 1.00001423355152 au
- Earth Perihelion: 0.983269342809232 au
- Moon
- Mass of the Moon: 0.01230314690256 Earth Masses (7.34767309E22 kg)
- Distance of Moon to Earth: 384400.0 km
- Radius of the Moon: 1737.1 km
L2 and the JWST
The James Web Space Telescope is located at L2 in the Earth-Sun system for several reasons. The first reason is that L2 is the furthest location from the Sun, Earth and Moon that is still continuously close enough to the Earth for easy communications. An orbit around the Sun, further from the Earth would drift away from the Earth and regularly be out of communications for long periods of time. A body in L2 will track with the Earth around the Sun. Furthermore, L2 is nearly 4x the distance of the Earth to the Moon. The Sun emits large amounts of light energy that could obscure what a highly sensitive telescope can see. That is why the JWST has such a large (4 layer) solar shield. Nonetheless, the JWST is solar powered. Again, L2 is inline with the Earth, but not so close that the Earth blocks the Sun's light. In short, L2 was a brilliant selection for the location of the James Web Space Telescope.
Astronomy Calculators
Astronomical Units
Because of the enormity of space and the size of the objects studied, the field of astronomy employs units not commonly used in everyday life. Nonetheless, these units do translate into common units at a grand scale, and vCalc provides automatic conversions between units for calculator inputs and answers via the pull-down menus. The following is a brief description on the distance, mass and time units employed in the field of astronomy
Astronomy Distance Units
Astronomical Unit (au): Within our solar system, a common measure of distance is au, which stands for astronomical units. A single astronomical unit is the mean distance from the Sun's center to the center of the Earth.
| Astronomical Unit (au) | Distance from Sun (au) |
|---|---|
|
|
Light Travel in Time: Light is a primary observable when studying celestial bodies. For this reason, the distance to these objects are measured in the amount of time it would take light to travel from there to the Earth. We can say that an object is one light-year away, and that means that the object is at a distance where it took an entire year for light from the object to travel to Earth. Since the speed of light is 299,792,458.0 meters per second, one can compute the distance equal to a light year as follows:
1 light year = 299,792,458.0 (meters / second) x 31,536,000 (seconds / year) = 9,460,528,405,000,000 meters
The same exercise can be used for light traveling shorter periods of times, light seconds, light minutes, light hours and light days. Since even these units are not enough when computing distances across the universe, there is also a light relative distance of kilo-light years (1000 light years), or the distance light travels in a thousand years!
| Light Second | Light Minute | Light Hour | Light Day | Light Year | Kilo-Light Year |
|---|---|---|---|---|---|
|
299,786 km 186,278 miles 0.002 au |
17,987,163 km 11,176,705 miles 0.12023 au |
1,079,229,797 km 670,602,305 miles 7.214 au |
25,901,515,140 km 16,094,455,343 miles 173.14 au |
9,460,528,405,000 km 5,878,499,814,210 miles 63,240 au 0.306 parsecs |
9,460,528,405,000,000 km 5,878,499,814,210,000 miles 63,240,000 au 306 parsecs |
Angle Shift Seen from Earth: Because the Earth goes around the Sun, our observation of distant objects such as stars results in an angular shift when observed at opposite sides of the elliptical orbit. This shift is used as the basis of a unit knows as a parsec. A parsec was traditionally defined as the distance where one astronomical unit subtends an angle of one arcsecond. A parsec was redefined in 2015 to 648000/π astronomical units. Proxima Centauri, is the nearest star to the Sun and is approximately 1.3 parsecs (4.2 light-years) from the Sun. A mega-parsec is a million parsecs.
| Parsec | Mega-parsec |
|---|---|
|
|
Astronomy Mass Units
Astronomical units also apply to the mass of enormous objects such as moons, planets and stars. For this reason, astronomy also employs mass units that compare other objects to ones familiar to us. For example, stars are often measured in mass units of solar masses. This is a comparison of their mass to the mass of our sun (one solar_mass). For planets, astronomers use Earth masses and Jupiter masses for understanding the relative size of rocky planets and gas giants.
| Earth Masses | Jupiter Masses | Solar Masses |
|---|---|---|
|
|
|
Astronomy Time Units
Astronomers use the same time units as everyone else, from the very small nanoseconds, to seconds, minutes, hours, days and years. This is true with two exceptions known as sidereal days and sidereal years. These refer to time relative to the celestial objects (the fixed stars). The Earth rotates every 24 hours relative to the Sun. But we are moving in a circle around the Sun. In comparison, the Earth rotates every 23 hours, 56 minutes and 4.0905 seconds (23.9344696 hours) compared to the stars in the celestial sphere. This is known as a sidereal day.
In the same vein, a sidereal year is the time it takes the Earth to complete one orbit around the Sun relative to the celestial sphere. Where a year is 365 days, a sidereal year is 365.256363004 days, or 1,224.5 seconds more than a calendar year.
| Sidereal Day | Sidereal Year |
|---|---|
|
|
- Comments
- Attachments
- Stats
No comments |