Disociación de fracciones de un ácido

La fracción de disociación de un ácido calcula la fracción de un ácido débil que se disocia en una solución y se utiliza en cálculos de ácido débil. 

Cómo se resuelve un problema de ácido débil:

Suponga que tiene una ecuación típica de reacción de disociación ácida y se le pide que resuelva el pH del ácido débil. La reacción típica de disociación ácida es 

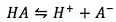  con su expresión de equilibrio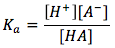  

Puesto que el ácido se disocia en una solución, también habrá una ecuación de equilibrio de agua

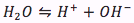 con su expresión de equilibrio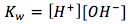

También podemos usar las ecuaciones de balance de masa y balance de carga para ayudarnos a resolver las incógnitas. 

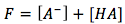 (balance de masa) 

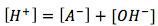(balance de carga)

Utilizando estas ecuaciones podemos encontrar el pH, pero primero debemos hacer algunas supsiciones. [A^-] y [H⁺] se producen cuando el ácido débil se disocia. Cuando el agua se disocia, se producen [OH^-] and [H⁺]. Cuando más HA está disociado en solución que el agua, podemos suponer que la concnetración [A^-] es mucho mayor que la de [OH^-], por lo que podemos excluir [OH^-]. Así, la ecuación del balance de carga se convierte en [H⁺]=[A^-]. Podemos conectar esto a la expresión de equilibrio anterior. Obtenemos la ecuación para los ácidos débiles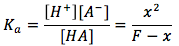. Al reordenar las variables podemos resolver para "x" que tambien es [A^-]=[H⁺] y conectralo a la ecuación del pH.

Descripción

La ecuación es 

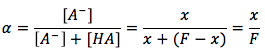
dónde

• x es la concentración de la partícula a2cida disociada [A^-] en unidades de (mol/L).
• F es la concentración formal en unidades de (mol/L).
• Alfa es la fracción de [A^-] disociada en la solución.

Temas Relacionados

• Balance de Masa (para el sitio en inglés haga clic aquí)
• Balance de Carga (para el sitio en inglés haga clic aquí)
• Ecuación para un ácido debil (para el sitio en inglés haga clic aquí)
• Constante de equilibrio ácido (para el sitio en inglés haga clic aquí)

Referencias

Harris, 9th Edition.  Pp.193