Moment of Inertia of a Beam Section

Last modified by

Jul 24, 2020, 6:28:07 PM

Created by

Feb 6, 2017, 3:20:42 AM

I_{beam section} = \sum ({\bar{I}}_{i} + A_{i} \cdot d_{i}^{2})

$I_("beam section") = sum(barI_i + A_i*d_i^2)$

(w_{1}) Top Flange Width

$(w_1) "Top Flange Width"$

(w_{2}) Vertical Width

$(w_2) "Vertical Width"$

(w_{3}) Bottom Flange Width

$(w_3) "Bottom Flange Width"$

(D_{1}) Top Flange Length

$(D_1) "Top Flange Length"$

(D_{2}) Vertical Length

$(D_2) "Vertical Length"$

(D_{3}) Bottom Flange Length

$(D_3) "Bottom Flange Length"$

Computing the Centroid of the Beam Section

We split the cross-section into into three segments, each segment having a nice rectangular symmetry. We then calculate the area and y-centroid of each of the three segments and compute the entire centroid as:

$\bar{y} = \sum \frac{A_{i} \cdot y_{i}}{\sum A_{i}}$ $bary = sum(A_i*y_i)/(sum A_i)$

The three segments are shown in the figure below, where $A_{i} = w_{i} \cdot D_{i}$ $A_i = w_i *D_i$ :

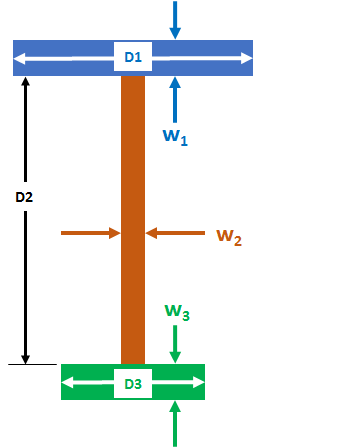
/attachments/3da0b692-ec1b-11e6-9770-bc764e2038f2/i-beam cross section.png

And the y-centroids of the segments are given as:

$y_{1} = w_{3} + D_{2} + \frac{w_{1}}{2}$ $y_1 = w_3 +D_2 + w_1/2$
$y_{2} = w_{3} + \frac{D_{2}}{2}$ $y_2 = w_3 +D_2/2$
$y_{3} = \frac{w_{3}}{2}$ $y_3 = w_3/2$

Computing the Moment of Inertia

Knowing the y-centroid of the beam's cross section computed above, we then compute the moment of inertia of each of the three segments sing the equation:

${\bar{I}}_{i} = \frac{{base}_{i} \cdot {height}_{i}^{3}}{12}$ $barI_i = ("base"_i * "height"_i^3)/12$

Then we find the distances, d_i, of the segment's centroid from the x-axis (the y-centroid we computed for the beam cross-section earlier).

$d_{i} = | y_{i} - \bar{y} |$ $d_i = |y_i - bary|$

The moment of inertia of the beam in cross-section is then given by:

$I_{(beam section)} = \sum ({\bar{I}}_{i} + A_{i} \cdot d_{i}^{2})$ $I_"(beam section)" = sum(barI_i + A_i * d_i^2)$

Moment of Inertia of a Beam Section

Computing the Centroid of the Beam Section

Computing the Moment of Inertia

See Also

Datasets

Equations and Data Items

Calculators

Equations and Data Items

Collections