Quantcast

HavDist DMS

Last modified by
on
Jul 29, 2024, 2:04:32 PM
Created by
on
Oct 12, 2021, 8:25:31 PM
`D = f(Lat1,Lon1,Lat2,Lon2)`
Toggle Units
`("Lat"_1) "Latitude Point 1"`
°
'
"
`("Lon"_1) "Longitude Point 1"`
°
'
"
`("Lat"_2) "Latitude Point 2"`
°
'
"
`("Lon"_2) "Longitude Point 2"`
°
'
"
Tags
Travel Haversine Navigation
UUID
8c00d747-2b9a-11ec-993a-bc764e203090

The Haversine Degrees, Minutes and Seconds calculator computes the distance between two points on a spherical model of the Earth along a great circle arc using points defined by degrees, minutes and seconds.  

INSTRUCTIONS: Enter the following:

  • (Lat1) Latitude Point 1
  • (Lon1) Longitude Point 1
  • (Lat2) Latitude Point 2
  • (Lon2) Longitude Point 2

HAVERSINE DISTANCE (D): The calculator returns the distance between the two points in kilometers.  However, this can be automatically converted to other distance units (e.g. miles or nautical miles) via the pull-down menu.

The Math / Science

The Haversine equation is used to determine the distance between two points (x and y) on the Earth based on a mean spherical earth radius.  The Haversine - Distance equation is important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes. It is a special case of a more general formula in spherical trigonometry, the law of haversines, relating the sides and angles of spherical triangles. The first table of haversines in English was published by James Andrew in 1805. Florian Cajori credits an earlier use by Jose de Mendoza y Ríos in 1801. The term haversine was coined in 1835 by Prof. James Inman.

The Haversine equation used in this calculator is:
 
     `D =  2 *sin^-1(sqrt(sin((lat2 - lat1)/2)^2 + sin((lon2 - lon1)/2)^2 * cos(lat1) * cos(lat2))) * mu_E`
where:
  • D = Great Circle Arc Length (distance)
  • lat 1 = latitude of first point
  • lon 1 = longitude of first point
  • lat 2 = latitude of second point
  • lon 2 = longitude of second point
  • `mu_E` = Mean Radius of the Earth (6371.009 km)

Sailing and Navigation Calculators:

Flight and Navigation Calculators

  • Correction Angle: Computes the navigation angle/azimuth correction angle using the wind speed, wind direction, flight heading and an Air Speed.
  • Ground Speed: Computes the ground speed based on the wind speed, wind direction, a Flight Heading and an Air Speed.
  • Haversine - Distance: Computes the distance between two points on a spherical model of the Earth along a great circle arc.  This also includes the rhumb line distance and azimuth for the rhumb line.
  • Travel Time between Coordinates: Computes the time to travel between to points on the globe in a great circle arc at an average velocity. 
  • Distance to Sea Level Horizon at Altitude: Computes the distance to the horizon from a specified height using a spherical model the mean spherical radius of the Earth
  • Force of Drag: Calculates the resisting force of drag on an object flowing through a medium (e.g. air).
  • Force of Lift: Computes the lifting force on the surface area of a wing based on the wing surface area, air flow velocity, density of air and a lift coefficient.
  • Lift Coefficient: Compute the lift coefficient of a wing based on lift force, wing surface area, wind speed and density of air.
  • Velocity Needed for Takeoff: Computes the velocity required to create more lift than the weight of an aircraft or watercraft using a wing (e.g. hydrofoil).
  • Glide Ratio: Computes the glide ratio based on the change in forward distance and the change in altitude.
  • Wing Surface Area: Computes the wing surface area required to achieve lift, base on a lift coefficient, lift force, wind speed and density of air.
  • Velocity of Air over the Wing: Computes the velocity required to achieve a lift, based on lift coefficient, lift force, wing surface area and density of air.
  • Air Speed from Pressures: It uses the Bernoulli Equation to estimate air speed based on the total Pressure measured by a pilot tube, total Static local atmospheric pressure and the Density of Air.
  • Center of Mass: Computes the vehicle center of mass between two loads (masses).

The haversine formula

For any two points on a sphere, the haversine of the central angle between them is given by

\operatorname{haversin}\left(\frac{d}{r}\right) = \operatorname{haversin}(\phi_2 - \phi_1) + \cos(\phi_1) \cos(\phi_2)\operatorname{haversin}(\lambda_2-\lambda_1)

where

  • haversin is the haversine function:

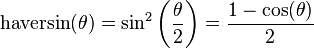
\operatorname{haversin}(\theta)=\sin^2\left(\frac{\theta}{2}\right)=\frac{1-\cos(\theta)}{2}

  • d is the distance between the two points (along a great circle of the sphere; see spherical distance),
  • r is the radius of the sphere,
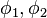  • \phi_1, \phi_2: latitude of point 1 and latitude of point 2
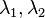  • \lambda_1, \lambda_2: longitude of point 1 and longitude of point 2

On the left side of the equals sign d/r is the central angle, assuming angles are measured in radians (note that φ and λ can be converted from degrees to radians by multiplying by π/180 as usual).

Solve for d by applying the inverse haversine (if available) or by using the arcsine (inverse sine) function:

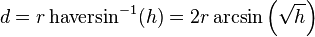
d = r \operatorname{haversin}^{-1}(h) = 2 r \arcsin\left(\sqrt{h}\right)

where h is haversin(d/r), or more explicitly:

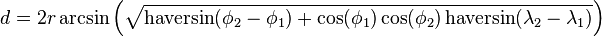
d = 2 r \arcsin\left(\sqrt{\operatorname{haversin}(\phi_2 - \phi_1) + \cos(\phi_1) \cos(\phi_2)\operatorname{haversin}(\lambda_2-\lambda_1)}\right)

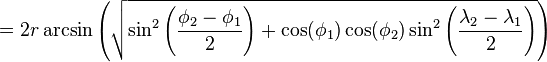
= 2 r \arcsin\left(\sqrt{\sin^2\left(\frac{\phi_2 - \phi_1}{2}\right) + \cos(\phi_1) \cos(\phi_2)\sin^2\left(\frac{\lambda_2 - \lambda_1}{2}\right)}\right)

When using these formulae, ensure that h does not exceed 1 due to a floating point error (d is only real for h from 0 to 1). h only approaches 1 for antipodal points (on opposite sides of the sphere) — in this region, relatively large numerical errors tend to arise in the formula when finite precision is used. Because d is then large (approaching πR, half the circumference) a small error is often not a major concern in this unusual case (although there are other great-circle distance formulas that avoid this problem). (The formula above is sometimes written in terms of the arctangent function, but this suffers from similar numerical problems near h = 1.)

As described below, a similar formula can be written using cosines (sometimes called the spherical law of cosines, not to be confused with the law of cosines for plane geometry) instead of haversines, but if the two points are close together (e.g. a kilometer apart, on the Earth) you might end up with cos (d/R) = 0.99999999, leading to an inaccurate answer. Since the haversine formula uses sines it avoids that problem.

Either formula is only an approximation when applied to the Earth, which is not a perfect sphere: the "Earth radius" R varies from 6356.752 km at the poles to 6378.137 km at the equator. More importantly, the radius of curvature of a north-south line on the earth's surface is 1% greater at the poles (≈6399.594 km) than at the equator (≈6335.439 km)— so the haversine formula and law of cosines can't be guaranteed correct to better than 0.5%. More accurate methods that consider the Earth's ellipticity are given by Vincenty's formulae and the other formulas in the geographical distance article.

The law of haversines

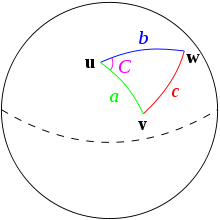/attachments/e6d11679-da27-11e2-8e97-bc764e04d25f/220px-Law-of-haversines.svg.pngSpherical triangle solved by law of haversines.

Given a unit sphere, a "triangle" on the surface of the sphere is defined by the great circles connecting three points u, v, and w on the sphere. If the lengths of these three sides are a (from u to v), b (from u to w), and c (from v to w), and the angle of the corner opposite c is C, then the law of haversines states:

(the law of haversines)

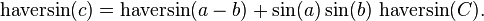
\operatorname{haversin}(c) = \operatorname{haversin}(a - b) + \sin(a) \sin(b) \, \operatorname{haversin}(C).

Since this is a unit sphere, the lengths a, b, and c are simply equal to the angles (in radians) subtended by those sides from the center of the sphere (for a non-unit sphere, each of these arc lengths is equal to its central angle multiplied by the radius of the sphere).

In order to obtain the haversine formula of the previous section from this law, one simply considers the special case where u is the north pole, while v and w are the two points whose separation d is to be determined. In that case, a and b are π/2 − φ1,2 (i.e., 90° − latitude), C is the longitude separation Δλ, and c is the desired d/R. Noting that sin(π/2 − φ) = cos(φ), the haversine formula immediately follows.

To derive the law of haversines, one starts with the spherical law of cosines:

(spherical law of cosines)

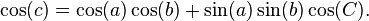
\cos(c) = \cos(a) \cos(b) + \sin(a) \sin(b) \cos(C). \,

As mentioned above, this formula is an ill-conditioned way of solving for c when c is small. Instead, we substitute the identity that cos(θ) = 1 − 2 haversin(θ), and also employ the addition identity cos(a − b) = cos(a) cos(b) + sin(a) sin(b), to obtain the law of haversines, above.

Navigation Calculators:

References

  • wikipedia - http://en.wikipedia.org/wiki/Haversine_formula
This equation, HavDist DMS, references 3 pages
This equation, HavDist DMS, is used in 1 page
  • Comments
  • Attachments
  • Stats
No comments
This site uses cookies to give you the best, most relevant experience. By continuing to browse the site you are agreeing to our use of cookies.