This vCalc version of the Bessel Function equation computes the solutions of Bessel's differential equation: 

`x^2 ((d^2y)/dx^2) + x(dy/dx) + (x^2 - nu^2) y = 0`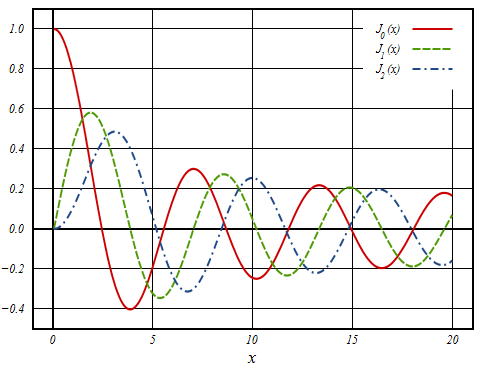

The plot of the first three orders of the Bessel Function of the first kind, corresponding to integer values of `nu`, is shown in the figure at the right.¹ 

Usage

The constant `nu` specifies the order of the Bessel Function and can be any real number. The set of solutions of an integer order (`nu = n`) are considered cylindrical problems and the set of solutions of any half integer order (`nu = n + 1/2`) are considered spherical problems.

This version of the Bessel Function of the first kind is expressed as an infinite series.  Since vCalc limits the processing time of equation execution, we must limit the number of terms we compute. the `k` input is the number of terms of the series that will be computed.  The processing time limit constrains us at the time of this equations creation to some number of terms less than 50.  The default has been set to 30 and that is sufficient to obtain a fairly accurate result.  The input `k` can be modified but its best top leave it at its default for now.

Derivation

Bessel's differential equation is a second order differential equation, which means there are two linearly independent solutions.  The solution is often given as:

`y= A*J_nu(x) + B*Y_nu(x)`, where `J_nu(x)` is a Bessel Function of the first kind and `Y_nu(x)` is a Bessel Function of the second kind. 

The Bessel Function of the second kind is sometimes known as a Weber Function or a Neumann Function.

Integral Versions

The infinite series for the Bessel function of the first kind estimated in this equation can also be derived as definite integrals.  Here is the general form of that definite integral:

`J_n(x) = 1/pi int_0^pi(cos(n*theta- xsin(theta)) d theta`

1. ^ Plot of Bessel Function of the first kind, J_nu(x), for the integer orders alpha = 0,1,2,...
   _{Wikipedia / Inductiveload  Public Domain}