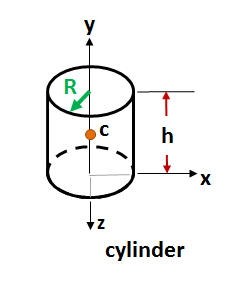
MoI - cylinder about x-axis
Tags | |
UUID | 94e9c852-fd6b-11e3-b7aa-bc764e2038f2 |
Mass Moment of Inertia
The Mass Moment of Inertia of a solid measures the solid's ability to resist changes in rotational speed about a specific axis. The larger the mass moment of inertia the smaller the angular acceleration about that axis for a given applied torque.
This equation computes the mass moment of inertia for a cylinder rotating about the x-axis as defined in the picture. The mass moment of inertia in this example is the same for rotations about both the x-axis and the z-axis due to symmetry.
Mass Moment of Inertia = (14mr2)+(13mh2)
Where the inputs are:
- m = mass of the entire body
- h = Height of a Cylinder
- R = Radius of the cylinder.
author: Carol
Notes
The mass moment of inertia varies, depending on the reference axis. And thus is often specified with two subscripts to clarify the specified axis. This helps to provide unique definition of rotational axis in three-dimensional motion where rotation can occur about multiple axes.
Calculators
- Comments
- Attachments
- Stats
No comments |
