This equation computes the mass of the Earth from what a flying pig tells us.  The pig is in flight, well actually tethered to a pole, and set in motion circling the pole in a horizontal plane.  Basically the pig is moving like a tether ball around the pole, only the rope is not wrapping as he circles.  If we measure the characteristics of the pig's location in flight, and the pig's mass, we can experimentally determine the mass of the Earth.

We know these constants in the equation:

• The Radius of the Earth (`R_e`), for instance, is 6378137.0 m   ( from the WGS-84 radius of the Earth constant in vCalc)
• The Universal Gravitational Constant (`G`) is 6.67384⋅10⁻¹¹ `m^3 /("kg"*s^2)`

We have three variables whose interrelationship is defined by the laws of gravity affecting the pig's circular motion:

• The radius of the circle the pig is rotating about
• The length of the tether attaching the pig to the pole
• The mass of the pig

The pig rotates with his tether sloping out and down from the pole (see picture below).  The faster he circles, the higher the horizontal plane he is circling in will rise. This is because the greater the rotation rate, the greater is the centripetal acceleration that generates the tension in the tether that offsets the gravitational attraction between the pig and the Earth.  As the pig rotates faster, he will rise, but it takes a lot of energy to make the pig rise very far. 

The Experiment

If you determine the pig's mass, set the pig in motion about the pole, measure the height of the tether while the pig is circling, and measure the radius of the circle, you can approximate the mass of the Earth (`M_e`) with this equation.  The estimated mass of the Earth should be:  `5.97219*10^24 " kg"`

A View of Our Flying Pig

I thought first in viewing professor Steve Spiklemire's YouTube video that a flying pig is a unique phenomena we really must explore.  When "pigs fly" echoes our contemporary knowledge that pigs are pretty much stuck to this Earth and that can lead us to ask how they are affected by that most fundamental physical phenomena, gravity.

This vCalc discussion was thus inspired by a video created by Steve Spicklemire, a professor at the University of Indianapolis.  The topic of that video was "Measuring the Mass of the Earth with a Flying Pig".

Now, in the past -- and continued today in modern science -- we have often found a need to measure physical attributes of the universe and the world around us to greater and greater precision.  We need to measure small things more accurately to differentiate the small from the smaller.  We need to more accurately measure the vastness of the cosmos so that we may more realistically make comparisons of the nearly-infinite to things that reside closer to home.  And thus we often devise comparative techniques, allowing us to compare in ratio something we can readily grasp to something that practically defies our limited logic.

The circular motion of a pig, though we collectively have probably never seen anyone harness a pig as described here, is realistically a possible avenue for determining the forces on a swinging pig and from this deriving the mass of the Earth, `M_e`.

Scientists have often found the best way to determine something as seemingly unobtainable as the total mass of the Earth is to measure something we know well and compare it geometrically to something whose dimensions we  have a hard time fathoming. We take a physical thing we can lay our hands on -  like a pig -- and we use its universally physical essences in a grandiose comparison.  We look at the slope of an anthill to conjecture what the likelihood is that the pyramids will withstand the constant tug of gravity for another millennia. We play with mirrors in the hallway to figure out how light travels across the vast emptiness of space.  And in this first case that professor Spicklemire depicts in video form, we look at how a pig can fly and, in so doing, measure the mass of our planet.

Well, OK, the pig in this thought experiment is not exactly "flying" but instead being swung in a circle like a tether-ball.  However, to the pig I am sure it feels as much like flying as a pig is capable of imagining. I still think of them, the harnessed pig, as pretty grudgingly incapable of higher reasoning.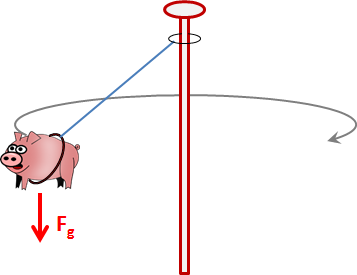

Picture this:  a pig strapped into a comfy harness (so as not to alarm animal rights activists) and this harness is tied to a rotating ring around the pole which enables the pig to be swung with some force that keeps the pig circling the pole for a given amount of experimental time at a constant angular velocity.

Yes, we give the pig a hefty push and he theoretically circles the pole in somewhat the same way you and I are swung around this sphere we call the Earth.  Can you feel it? we're traveling approximately 1100 (in instantaneous velocity), depending on exactly what latitude you are on the planet's surface.  And we also feel that tug toward the center of our rotation that is the net force of our being tethered to the Earth by gravity.  And our theoretical pig is, in addition to experiencing the pull of gravity downward, being swung around a pole in a big circle and feeling an additional pull along the line of the rope.

Now, harken back to a time on the playground era of your childhood if you cannot picture the pig circling the pole. Remember how the ball that you swung with all your might would circle high above the head of your opponent? and when you tired and and imparted less force to the ball, the ball swung slower dipped lower?  Remember that?

You were seeing the effect of the forces generated by swinging that ball -- just like the pig in our thought experiment -- in a circle at some velocity, `vecv`. We are talking "instantaneous velocity" because velocity, in the case of a circling object, is always changing its vector direction. The velocity we recognize as keeping the ball or pig aloft is that vector velocity at that exact instant of time where we capture our thought of the rotating, almost-flying, pig.

Remember, the faster the pig circles, the higher he will rise, just like the tether ball of your childhood competitive experience.  The rope we tied to the pig's harness tugs with a tension, `F_t`, on the pig.  Swinging the pig creates this force in the rope and the vertical component, `F_(t_y)` offsets the invisible force of gravity we show above as `vecF_g`.  The faster we swing the pig, the greater the tension in the rope connecting him, albeit loosely, to the pole.