Golden Ratio Sequence

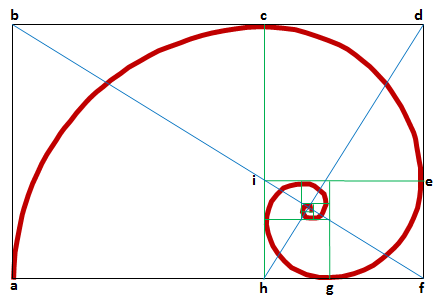
The basis for this equation has been publicized since the 1500s and is related directly to the famed Fibonacci sequence .  This equation computes the longer side of a rectangle if you input the shorter side and continues to use the result longer side as the input shorter side, generating a sequence of successively larger values.  The resultant rectangle defined by any two of these adjacent sequence values is a "golden rectangle," adhering to the rule that (a+b)/a = a/b = `phi`, where phi is the golden ratio.

The out put is n + 1 of these values in golden ratio, starting with whatever value you wish to input.