The Effect of Wind at a College Stadium calculator is in honor of the momentous milestone in professional football that is the 50th anniversary of the Superbowl. This vCalc equation computes an estimated distance a pass travels considering the effect of wind conditions in a particular stadium.  You can select your own choice of stadium but the Levi's Stadium, which is the site of the 50th anniversary Superbowl, is the first choice.

The Football's Trajectory

When the quarterback throws the ball it becomes a ballistic projectile.  Once the ball leaves the quarterback's fingers, it follows a ballistic trajectory, the same as a cannon ball or a bullet - to a first approximation.  All the force is applied as the quarterback's arm goes forward and when he releases the ball it is thereafter subject only to Newton's Laws and the force of gravity (to a first approximation¹ ). Sportscasters are not too far off when they use the analogy that the quarterback's arm "is a cannon".

Your Inputs to the Equation

Initial Pass Velocity

To determine the pass distance we have to know the initial velocity of the football.  This is the hardest thing in this equation to estimate, as the pass velocity varies greatly between those "bullet-like" missiles the quarterback throws when he is trying to stab the football in between two defenders and the touch pass lob to the back of the end zone, between the easy backward pass to a running back swinging toward the sideline out of the backfield and the "rocket" fired at the slanting tight end just beyond the line of scrimmage.

We've found estimates of the fastest football passes thrown by a passer being in the vicinity of 50 mph.  We have set the default value this assumed 50 mph maximum, so if you don't change the default ball speed, the equation will use 50 mph, a very powerful pass.  You are free to set the value to whatever initial velocity you please.

Pass Direction

In addition to the ball's initial speed at release, we ask you for the direction of the ball which you specify as an angle from the center-line of the field (or the angle from the direction parallel to either sideline. We need to know the pass direction because the interaction with the wind direction will vary, depending on the direction the pass is thrown.  

Velocity is a vector quantity.  That means it has both speed and direction.  Your speedometer tells you at what speed you are traveling in your car but when you're heading at 70 mph north on the freeway, that is stating your vector velocity.  If you're traveling at 70 mph on your neighborhood street, that is trouble.

Goal Direction

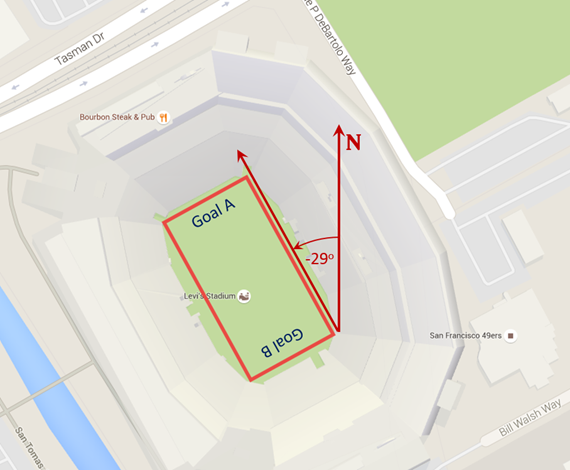
The ball's direction relative to the field must take into account the direction the offense is moving toward their goal. The Levi's Stadium's sideline run close Southeast to the Northwest (actual measured angle of the sidelines is -29 degrees from North, where the angle is measured negative counterclockwise).  So, the offense can be heading to the northwest (more north than west) or they can be heading toward the opposite goal to the southeast. This equation gives you the option of choosing the Goal direction as "Goal A" or :Goal B" as designated in the pictures below of the stadiums.  In general the northernmost or easternmost ends of a stadium will be designated "Goal A," but check the images below to be sure.

We have given you the selectable option to be moving toward either goal in your chosen stadium.  We have embedded the orientation of the stadium's sidelines in a vCalc data set from which we grab the orientation of the stadium you choose.  That vCalc data set is the NFL Stadium Orientation.

The orientation of the  Levi's Stadium is -29^o from North. Using the Stadium's orientation and the angle of the pass from the playing field's lengthwise center line, we can add the effect of the reported wind direction on the pass's ballistic trajectory approximation. 

Wind's Velocity

We have to know the wind's direction and speed to determine the wind's impact on the pass.  Usually the announcers will tell us this in pre-game banter or we can look it up on a weather site for the location of the stadium. 

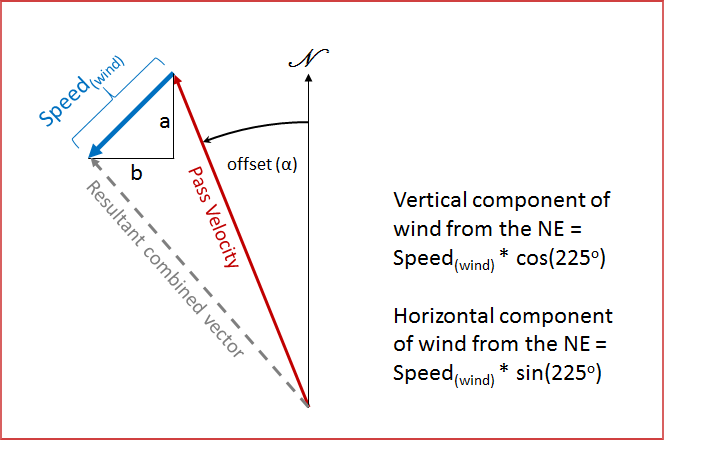
We combine the two velocity vectors for the wind and the football by translating them both into angles from North.  In other words we're calling the direction down the middle of the field the vertical for the sake of orienting the pass direction to include the field's offset angle from North.  The offset angle of the field center line is that angle shown in the pictures of the stadiums.  Once we determine the angle of the pass from North and add to that the angle of the wind direction, which is given as an angle from North, we can compute a combined velocity vector for the pass affected by wind.

The wind velocity (in vector form) is added to the ball's velocity in the horizontal plane.  Note this is a simplifying assumption that the wind bows horizontally.  The easiest way to add the pass trajectory to the wind's vector is by adding the vertical and horizontal components of the two velocity vectors.  See the picture above where the horizontal and vertical components of the wind velocity vector are shown labeled 'a' and ab'.  We add the vertical component of the football's velocity and the vertical component of the wind.   We add the horizontal component of the football's velocity and the horizontal component of the wind.  The summed horizontal component and the summed vertical component represent the components of the total pass vector in the horizontal plane 

Combining Wind and Pass Velocities

The resulting components, the combined horizontal or vertical components of the wind and pass velocities, will tell us a lot of things about a passing game.  If the wind is blowing in the opposite direction to a long pass thrown down the center of the field, we can compute the maximum distance the quarterback is able to throw a pass directly into the wind.  This assumes of course we can estimate the maximum velocity the quarterback will give to his long ball.

In the case of the passer being a leading passer, we can expect the maximum velocity of a pass to be somewhere near 50 mph leaving his hand.  Since we are approximating the pass as a ballistic trajectory, we can assume the longest pass will be thrown at around a 45 degree angle leaving the quarterback's hand.  

The maximum distance of a ballistic trajectory leaving and returning to the same horizontal plane is always traveled if the launch angle is 45 degrees.  In this equation we assume the receiver will catch the ball  at approximately the same height as the quarterback's release of the ball.  The ballistic equation used inside this "Effect of the wind on a pass" will compute the longest pass possible if the receiver is able to dive with outstretched hands and just manage to snag the ball at about shoulder height.  And again, this equation neglects air drag, the torque due to the spin the quarterback applies to the ball, surface texture of the pigskin, wind velocity component in the vertical dimension.

We will add all these additional factors in subsequent equations.  See the vCalc Football Collection for additional versions of this calculation.

Stadium's Orientation

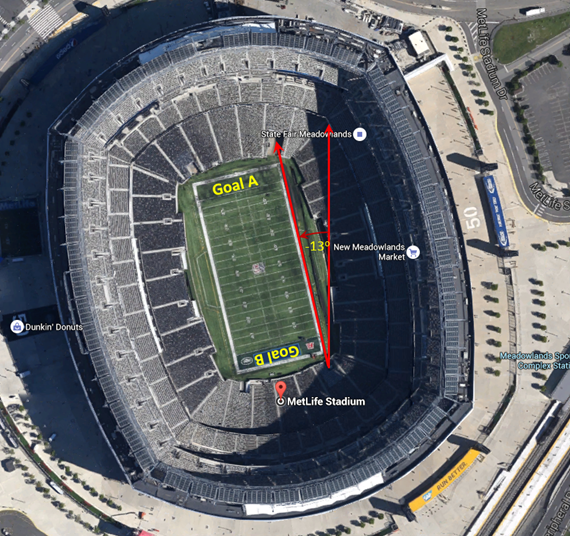
To determine the orientation of the lengthwise center line of the NFL Stadiums relative to North (which again we recorded in the vCalc data set, , we used Google Map views of the Stadiums.  Google Maps general does a good job of providing an overhead shot of the stadium that is close enough to straight overhead to allow us to measure relatively accurately the angle of the sidelines from North. You can see our stadium orientation approximation method applied to the individual stadium Google Maps views below.

Using this Equation

Specify the Goal Direction and the Wind Direction

We have given you the selectable option to be moving toward either goal in your chosen stadium.  You specify the direction that the quarterback would be facing at the line of scrimmage by choosing the goal the offense would be facing as Goal A or Goal B.  The center line is then perpendicular to the goal line and the pass angle is specified as an angle from this.  It is easiest to use the clockwise as positive and counter-clockwise as negative representation of angle. So for example, if the center line of the field runs North and South and the offense is facing the northern goal, then a sideline pass to the East would be 90 degrees and a sideline pass to the West would be -90 degrees.

Winds are often specified as coming from one of the compass points.  So, in this vCalc equation you select one of the following for direction from which the wind is coming:

• north (N)
• north northeast (NNE)
• northeast (NE)
• east northeast (ENE)
• east (E)
• east southeast (ESE)
• southeast (SE)
• south southeast (SSE)
• south (S)
• south southwest (SSW)
• southwest (SW)
• west southwest (WSW)
• west (W)
• west northwest (WNW)
• northwest (NW)
• north northwest (NNW)

If for example the wind is reported out of the Southwest, that means it is heading to the Northeast, which would make it's wind vector direction 45 degrees from North.

Finding the Longest Pass Possible

To determine the longest pass possible given the wind direction, try a launch angle of around 45 degrees.  You can change the pass direction to take advantage of the wind but if you have the reported wind direction, the angle of the pass and the launch angle will have the most visible affect on the length of the pass.

Gauging the Touch Pass

To look at the velocity of the touch pass, picture the quarterback having to throw over the outstretched hands of several big defensive linemen.  If the quarterback is three yards back in the pocket when he throws the ball and the receiver is three yards beyond the line AND the defensive linemen can reach easily to 9 feet, then the quarter back has to make a fairly easy pass to arc over the defensive line and get the ball to drop into that crossing receiver.

Stadium Goal Selection

Ok, for the stadium of your choice shown below, you must select the goal as depicted in the diagrams of the stadium.  You select Goal 1 or Goal 2. Generally Goal 1 is the northernmost or easternmost end of the stadium when the sidelines run more to the north or the east respectively.

Levi's Stadium	Metlife Stadium

1. ^ to a first approximation, we can ignore the effect of air drag on the football and the Coriolis affect caused by the rotation of the Earth, though these factors do have some affect on the total flight path of a football