Processing...
`θ = 2 cos^-1(( "r" - "h" )/ "r" )`
Enter a value for all fields
The Angle of a Circle Arc from Radius and Chord Depth calculator computes the angle of a segment of a circle defined by arc segment area
arc segment area 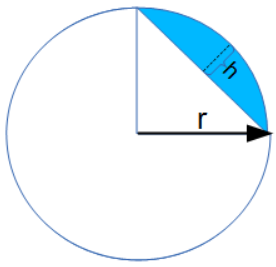 the radius of the circle (r) and the max distance (h) that the chord reaches away from the edge of the circle.
the radius of the circle (r) and the max distance (h) that the chord reaches away from the edge of the circle.
INSTRUCTIONS: Choose your preferred units and enter the following:
- (r) Radius of Circle
- (h) Depth of Chord
Arc Angle(θ): The angle of the arc segment is returned in radians. However, this can be automatically converted to other angle units via the pull-down menu.
The Math / Science
The formula for Angle of a Circle Arc is as follows:
θ = 2 • cos-1( (r-h)/r)
where:
- θ = angle of the circle defining the arc
- r = circle radius
- h = depth of chord
Circle Calculators
- Circle Area - Computes the area of a circle given the radius (A = π r2).
- Area of Circle Arc Segment f(r,θ) - Computes the area of an arc segment of a circle given the radius (r) and angle (θ)
- Area of Circle Arc Segment Area f(r,h) - Computes the area of an arc segment of a circle given radius (r) and the depth (h) into the circle.
- Area of Circle Sector f(r,Θ) - Computes the area of a sector (pie slice) of a circle given the radius (r) and angle (Θ).
- Angle of Circle Sector f(r,h) - Computes the angle in a circle from the radius and depth of the chord.
- Area of Circle Annulus - Computes the area of an annulus (ring) given the inner radius (r) and outer radius (R).
- Radius of Circle from Center and a Point - Computes the radius of a circle given the center point (h,k) and any other point (x,y) on the circle.
- Circumference of Circle - Computes the circumference of a circle given the radius (C = 2 π r).
- Circle Arc Length - Computes the length of an arc length on a circle given the radius (r) and angle (Θ)
- Circle within a Triangle - Computes the radius of a circle inscribed within a triangle given the length of the three sides (a,b,c) of the triangle.
- Circle around a Triangle - Computes the radius of a circle that circumscribes a triangle given the length of the three sides (a,b,c) of the triangle.
- Circle Diameter from Area - Computes the radius and diameter of a circle from the area.
- Circle Radius from Circumference - Computes the radius of a circle given the circumference.
- Circle Circumference from Area - Computes the circumference of a circle given the area.
- Circle Radius from Area - Computes the radius of a circle given the area.
- Chord Length: Computes the length of a chord in a circle from the radius and height.
- Chord Length from Arc Length and Radius: Computes the length of a chord on a circle based on the circle's radius (r) and the length of the arc (a).
- Circle Radius from Chord - Computes the radius of a circle based on the length of a chord and the chord's center height.
- Circle Equation from Center and one Point - Develops the general equation of a circle based on the coordinates of the center (h,k) and any point on the circle (x,y).
- Circle Equation from Three Points: Develops the general equation of a circle that goes through three points that are not in a straight line.
- Circle with same Perimeter as an Ellipse - Computes the radius of the circle with the same perimeter of an ellipse defined by the semi-major and semi-minor axes.
- Rectangles to Cover a Circle - Computes the number of rectangles needed to minimally cover a circle based on the circle's diameter and the length and width of the rectangles.