Tags | |
The Force Vector Addition calculator computes the magnitude of a resulting force based on two forces and the angle between them.
INSTRUCTIONS: Choose units and enter the following:
- (A) Magnitude of Vector A
- (B) Magnitude of Vector B
- (θ) Angle between Vectors A and B
Result Vector (C): The calculator returns the magnitude of vector C in Newtons and the angle (α) in degrees. However, these can be automatically converted to compatible units via the pull-down menu.
The Math / Science
The formula for the addition of two force vectors is:
`|C| = sqrt( (B sin(θ))^2 + (A + B cos(θ))^2)`
α = asin( y / C)
where:
- α is the resulting vector angle
- y is the resulting vector vertical offset
- C is the sum of the two force vectors
- A is the first force vector
- B is the second force vector
- θ is the angle between them.
3D Vector Functions
 k⋅V - scalar multiplication
k⋅V - scalar multiplication- V/k - scalar division
- V / |V| - Computes the Unit Vector
- |V| - Computes the magnitude of a vector
- U + V - Vector addition
- U - V - Vector subtraction
- |U - V| - Distance between vector endpoints.
- |U + V| - Magnitude of vector sum.
- V • U - Computes the dot product of two vectors
- V x U - Computes the cross product of two vectors
- V x U • W - Computes the mixed product of three vectors
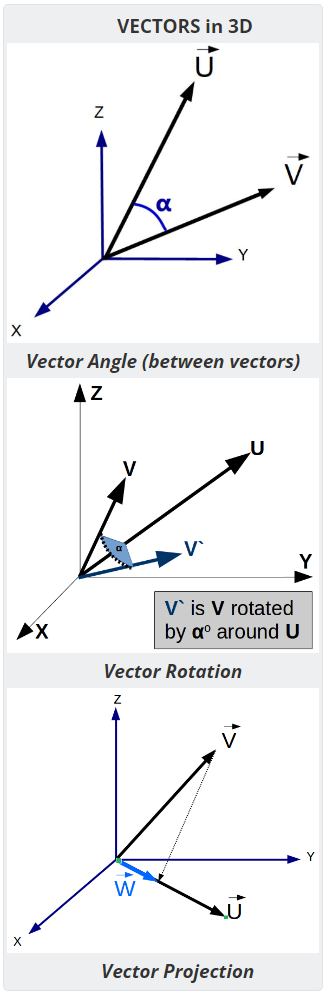
- Vector Angle - Computes the angle between two vectors
- Vector Area - Computes the area between two vectors
- Vector Projection - Compute the vector projection of V onto U.
- Vector Rotation - Compute the result vector after rotating around an axis.
- Vector Components 3D - Returns a vector's magnitude, unit vector, spherical coordinates, cylindrical coordinates and angle from each axis.
- (ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
- (x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
- (r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
- (x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
- (x,y) to (r, θ) - Cartesian to Polar
- (r, θ) to (x,y) - Polar to Cartesian
- Vector Normal to a Plane Defined by Three Points
