pH and pOH

A pH scale is a measure of how acidic or basic a substance is. While the pH scale formally measures the activity of hydrogen ions in a substance or solution, it is typically approximated as the concentration of hydrogen ions. However, this approximation is applicable only under low concentrations.

Self-Ionization of Water

The pH scale is logarithmic, meaning that an increase or decrease of an integer value changes the concentration by a tenfold. For example, a pH of 3 is ten times more acidic than a pH of 4. Likewise, a pH of 3 is one hundred times more acidic than a pH of 5. Similarly a pH of 11 is ten times more basic than a pH of 10. Because of the amphoteric nature of water (i.e., acting as both an acid or a base), water does not always remain as H₂O. In fact, two water molecules react to form hydronium and hydroxide ions:

`2H_2O(l)  ->  H_3O^(+) (aq) + OH^(-) (aq)`

This is also called the self-ionization of water. The concentration of H₃O⁺ and OH^- are equal in pure water because of the stoichiometric ratio. The molarity of H₃O⁺ and OH^- in water are also both 1.0×10^-7M at 25° C. Therefore, a constant of water (Kw) is created to show the equilibrium condition for the self-ionization of water. The product of the molarity of hydronium and hydroxide ion is always 1.0×10^-14.

`k_w = [H_3O^(+)][OH^(-)] = 1 * 10^(-14)`

This equations also applies to all aqueous solutions. However, Kw does change at different temperatures, which affects the pH range discussed below. Note: H⁺ and H₃O⁺ is often used interchangeably. The equation for water equilibrium is:

`H_2O  ->  H^(+) + OH^(-)`

• If an acid (H⁺ ) is added to the water, the equilibrium shifts to the left and the OH^- ion concentration decreases
• If base ( OH^-) is added to water, the equilibrium shifts to left and the H⁺ concentration decreases. 

pH and pOH

Because the constant of water, K_w is always 1.0 X 10^-14, the pK_w is 14, the constant of water determines the range of the pH scale. To understand what the pK_w is, it is important to understand first what the "p" means in pOH, and pH. The danish biochemist Soren Sorenson proposed the term pH to refer to the "potential of hydrogen ion."  He defined the "p" as the negative of the logarithm, -log, of [H⁺]. Therefore the pH is the negative logarithm of the molarity of H. The pOH is the negative logarithm of the molarity of OH^- and the pK_w is the negative logarithm of the constant of water. These definitions give the following equations:

`pOH=-log([OH^-])`
`pK_w= -log [K_w]`

A Logarithm, used in the above equations, of a number is how much a power is raised to a particular base in order to produce that number. To simplify this, look at the equation: log_ba=x. This correlates to b^x=a. A simple example of this would be log₁₀100=2, or 10²=100. It is assumed that the base of Logarithms is ten if it is not stated. So for the sake of pH and pOH problems it will always be ten. When x is a negative number that means you are dividing it by the power. So, if log₁₀0.01=-2 which can be written 10^-2=0.01. 10^-2 also means 1/10². The log function can be found on your scientific calculator. Now if we apply this to pH and pOH we can better understand how we calculate the values.

The constant of water is always 1.0 X 10^-14. So pK_w=-log [1.0 X 10^-14]. Using what we know about Logarithms, we can write this as 10^-pK_w=10^-14. By substituting we see that pK_w is 14. The equation also shows that each increasing unit on the scale decreases by the factor of ten on the molarity. For example, a pH of 1 has a molarity ten times more concentrated than a solution of pH 2. Also, the pK_w of water is 14 and the addition of pH and pOH is always 14 at 25° Celsius.

`pK_w=pH+pOH`=14

Range of pH and how to read it

The pH scale is often referred to as ranging from 0-14 or perhaps 1-14. Neither is correct. The pH range does not have an upper nor lower bound, since as defined above, the pH is an indication of concentration of H⁺. For example, at a pH of zero the hydronium ion concentration is one molar, while at pH 14 the hydroxide ion concentration is one molar. Typically the concentrations of H⁺ in water in most solutions fall between a range of 1 M (pH=0) and 10^-14 M (pH=14). Hence a range of 0 to 14 provides sensible (but not absolute) "bookends" for the scale. However, in principle, one can go somewhat below zero and somewhat above 14 in water, because the concentrations of hydronium ions or hydroxide ions can exceed one molar. Figure 1 depicts the pH scale with common solutions and where they are on the scale. 

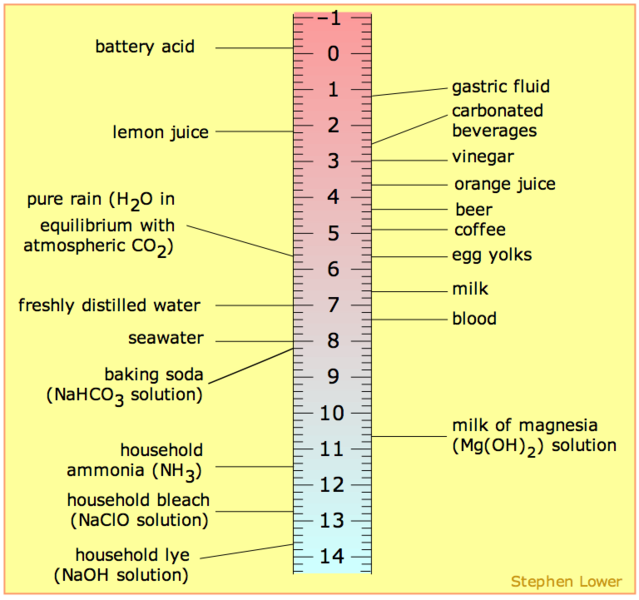
Figure 1: Solutions and the placement of them on pH scale

• From the range 7-14, a solution is basic. The pOH should be looked in the perspective of OH^- instead lf H⁺. Whenever the value of pOH is greater than 7, then it is considered basic. And therefore there are more OH^- than H⁺ in the solution   

• At pH 7, the substance or solution is at neutral and means that the concentration of H⁺ and OH^- ion is the same.

• From the range 1-7, a solution is acidic. So, whenever the value of a pH is less than 7, it is considered acidic. There are more H⁺ than OH^- in an acidic solution.                                                                               

Example 1
If the concentration of NaOH in a solution is 2.5 X 10-4 M, what is the concentration of H3O+?

Worked Problem Here

 

Example 2
1) Find the pH of a solution of 0.002M of HCl. 2) Find the pH of a solution of 0.00005M NaOH. Worked Problem Here

Example 3
If soil has a pH of 7.84, what is the H+ concentration of the soil solution? Worked Problem Here Subpages (1): Examples 1, 2, and 3