The Area of Hexagon calculator computes the area of a regular Hexagon.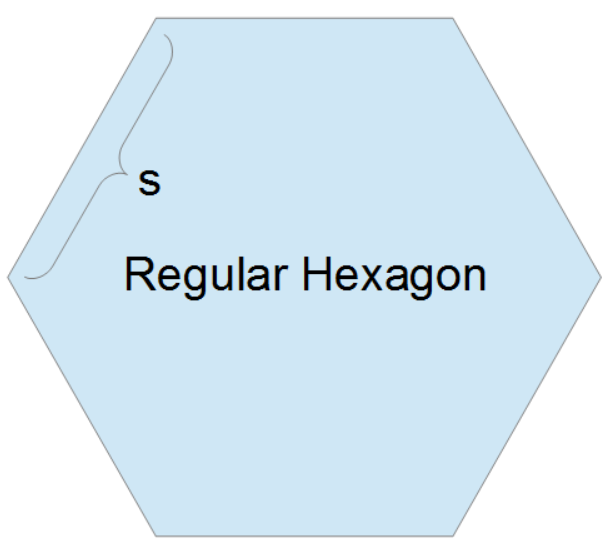
INSTRUCTIONS: Choose units and enter the following:
- (s) Side Length
Area of the Hexagon (A): The calculator returns the area in square meters. However, this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
A regular hexagon is a six sided polygon where all of the sides are the same length (s) and all interior angles are the same (see the diagram). The formula for the area of a hexagon is:
`A=3/2 * sqrt(3) * s^2`
where:
- A is the area of the hexagon
- s is the length of one side of the regular hexagon
A hexagon is a polygon with six sides and six angles. It is a two-dimensional geometric shape formed by connecting six straight line segments (sides) in a closed loop. Each interior angle of a regular hexagon
(where all sides and angles are equal) measures 120 degrees. The sum of the interior angles in any hexagon is 720 degrees.
Hexagon Calculators
- Hexagon Area: Area of regular hexagon based on length of sides
- Hexagon Side Length from Area: Length of a regular hexagon's sides based on the area.
- Hexagon Volume: Volume of Hexagon Column based on dimensions.
- Hexagon Column Surface Area: Surface area of Hexagon Column based on dimensions.
- Hexagon Column Mass: Mass or weight of Hexagon Column based on dimensions and density.
- Sum of Hexagon Areas: Surface Area of interconnected hexagons based on side length and number of hexagons.
- Hexagon Planter: Volume and surface area of a hexagon shaped planter and the amount of soil needed to fill it.
Hexagons in Nature and Science
Hexagons are encountered in various natural and man-made contexts. In nature, honeycombs constructed by bees often exhibit a hexagonal pattern because it is an efficient way to fill space with the least amount of material. In geometry and design, hexagons are commonly used in patterns, tiling, and architectural structures. They also appear in everyday objects, such as nuts and bolts, and are widely used in fields like science, engineering, and mathematics.
Giant's Causeway's hexagons: Using this equation and the fact that the shoe in the picture is approximately 12" long and that the side of the hexagon is approximately the length of the shoe, the AREA of these regular hexagons is 2.5 ft2.
Hexagons were also used by NASA in the James Webb Space Telescope.
Image provide by: Bobarino - Own work based on: File:JWST-HST-primary-mirrors.jpg a NASA public domain image, CC BY-SA 3.0
The side of each JWST is approximately 0.737 meters. Use the sum of hexagon areas (CLICK HERE) to compute the total area of the 18 hexagon mirrors. The primary mirror of the Hubble Space Telescope is 2.4 meters in diameter. Use the area of a circle calculator (CLICK HERE) to compute the area of the Hubble Space Telescope primary mirror.
Regular Polygon Information
A regular polygon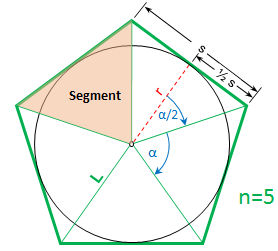
is a geometric shape with three or more straight sides where every side is the same length and every angle between connecting sides are the same angle. Because of the symmetry of the regular polygon, all the vertices of the polygon can be constructed to touch a circle in which the regular polygon is inscribed and all the chords that are polygon sides will then obviously be of equal length . Likewise, because of the regular polygon's symmetry, a circle constructed to be inscribed in a regular polygon and touching the polygon will touch the regular polygon at the midpoint of the polygon side. As shown in the pictures, Figure 1 and Figure 2, lines from the regular polygon's vertices to the circle's center form n isosceles triangles of equal area.
The names of polygons vary based on the number of sides as follows:
- triangle - 3 sides
- square - 4 sides
- pentagon - 5 sides
- hexagon - 6 sides
- heptagon - 7 sides
- octagon - 8 sides
- nonagon - 9 sides
- decagon - 10 sides
- hendecagon - 11 sides
- dodecagon - 12 sides
Common Regular Polygon Functions
Polygon Area Calculators:
- Polygon Area from the Number of sides and Length of Sides
- Polygon Area from the Number of Sides and Outside Radius
- Area of a Polygon Segment (triangle) from the Number of Sides and Inscribed Radius
- Polygon Area from the Number of Sides and Inscribed Radius.
Polygon Side Calculators
- Length of a Polygon Side from the Number of Sides and Outer Radius
- Length of a Polygon Side from the Number of Sides and Inner Radius
- Length of a Polygon Side from the Number of Sides and Area in Poloygon
Polygon Perimeter Calculators
- Perimeter of a Polygon from Number of Sides and Length of Sides
- Perimeter of a Polygon from Number of Sides and Outer Radius
- Perimeter of a Polygon from Number of Sides and Inner Radius
- Polygon Perimeter from the Area and Number of Sides
Polygon Radius
3D Polygon Shapes
Other Polygon Calculators
- Interior Angle of a Regular Polygon based on the number of sides
- Area of Circle - Circle approximates a polygon as the number of sides approaches infinity.
- Area of Triangle - Three Sides
- Area of a Square - Four Sides
- Area of Pentagon - Five Sides
- Area of Hexagon - Six Sides
- Area of Heptagon - Seven Sides
- Area of Octagon - Eight Sides
- Area of Nonagon - Nine Sides
- Area of Decagon - Ten Sides
- Area of Hendecagon - Eleven Sides
- Area of Dodecagon - Twelve Sides