This Area of a Circle Arc Segment calculator computes the area of a segment of a circle defined by the radius of the circle (r) and the max distance (h) that the chord reaches away from the edge of the circle. 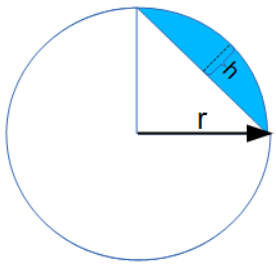
INSTRUCTIONS: Choose units and enter the following:
- (r) Radius of Circle
- (h) Depth of Chord from Edge of Circle
Area of a Circle Arc Segment (A): The area (A) returned in square inches. However, this can be automatically converted to other area units via the pull-down menu.
The Math
The formula for Area of a Circle Arc Segment is as follows:
where
- A = Area of Circle Arc Segment
- r = radius of the Circle
- θ = angle swept
This calculator uses the formula above with the following substitution:
θ = 2 * acos( (r-h)/r)
where:
- θ = angle in the circle
- r = radius of the circle
- h = max depth of the chord
See Also
A related equation provides the same area if the angle defining the arc chord (θ) is known: To compute the area of the arc segment of a circle using the angle (θ) and radius (r), CLICK HERE.
Circle Calculators
- Circle Area - Computes the area of a circle given the radius (A = π r2).
- Area of Circle Arc Segment f(r,θ) - Computes the area of an arc segment of a circle given the radius (r) and angle (θ)
- Area of Circle Arc Segment Area f(r,h) - Computes the area of an arc segment of a circle given radius (r) and the depth (h) into the circle.
- Area of Circle Sector f(r,Θ) - Computes the area of a sector (pie slice) of a circle given the radius (r) and angle (Θ).
- Angle of Circle Sector f(r,h) - Computes the angle in a circle from the radius and depth of the chord.
- Area of Circle Annulus - Computes the area of an annulus (ring) given the inner radius (r) and outer radius (R).
- Radius of Circle from Center and a Point - Computes the radius of a circle given the center point (h,k) and any other point (x,y) on the circle.
- Circumference of Circle - Computes the circumference of a circle given the radius (C = 2 π r).
- Circle Arc Length - Computes the length of an arc length on a circle given the radius (r) and angle (Θ)
- Circle within a Triangle - Computes the radius of a circle inscribed within a triangle given the length of the three sides (a,b,c) of the triangle.
- Circle around a Triangle - Computes the radius of a circle that circumscribes a triangle given the length of the three sides (a,b,c) of the triangle.
- Circle Diameter from Area - Computes the radius and diameter of a circle from the area.
- Circle Radius from Circumference - Computes the radius of a circle given the circumference.
- Circle Circumference from Area - Computes the circumference of a circle given the area.
- Circle Radius from Area - Computes the radius of a circle given the area.
- Chord Length: Computes the length of a chord in a circle from the radius and height.
- Chord Length from Arc Length and Radius: Computes the length of a chord on a circle based on the circle's radius (r) and the length of the arc (a).
- Circle Radius from Chord - Computes the radius of a circle based on the length of a chord and the chord's center height.
- Circle Equation from Center and one Point - Develops the general equation of a circle based on the coordinates of the center (h,k) and any point on the circle (x,y).
- Circle Equation from Three Points: Develops the general equation of a circle that goes through three points that are not in a straight line.
- Circle with same Perimeter as an Ellipse - Computes the radius of the circle with the same perimeter of an ellipse defined by the semi-major and semi-minor axes.
- Rectangles to Cover a Circle - Computes the number of rectangles needed to minimally cover a circle based on the circle's diameter and the length and width of the rectangles.