Phase Angle (AC)
This equation computes the Phase Angle, `phi`.
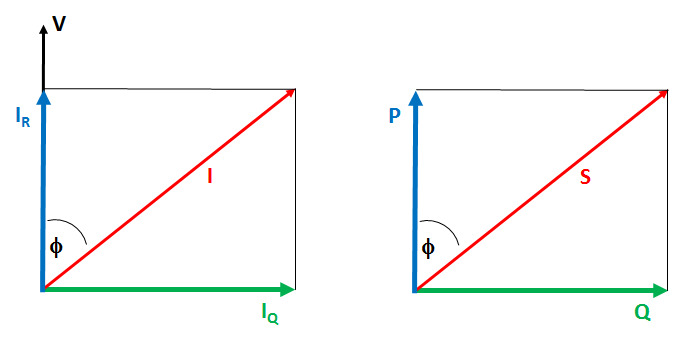
The Phase angle is the angle between the active component of the current, `vecI_R`, (which is parallel to the Voltage, V), and the current, `vecI`.
The inputs to this equation are: `I_R` and `I`
Notes
The instantaneous electric power in an AC circuit is given by `P = V*I`. These quantities, V and I, are continuously varying. The average power in an AC circuit is given by `P_"avg" = V*I*cos(phi)`, where
`phi` = is the phase angle between the current and the voltage
In alternating current circuits, the current can be represented by two components:
the active component `I_R`, in phase with the supply voltage, V, the active component of the current is directly correlated to the electrical energy output. This is the energy converted to heat or light or mechanical energy.
the reactive component IQ, which in quadrature to the voltage (separated by 90 degrees in phase), produces the flow of current.
In the presence of ohmic-inductive loads, the total current, I, lags the active component `I_R`.
The Power Factor (cos`phi`) is defined as the ratio between the active component `I_R`.
and the total value of the current l.
The angle `phi` is the phase difference between the voltage, V, and the current, l, so that `cos(phi) = I_R/I = P/S`
In the diagram, the active power is P and the reactive power is Q.The apparent power is S.