Angle of a Circle Arc from Radius and Chord Depth

The  Angle of a Circle Arc from Radius and Chord Depth calculator computes the angle of a segment of a circle defined by arc segment area 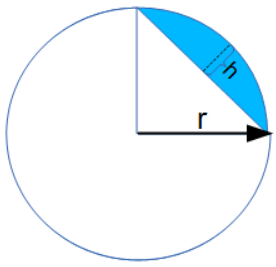 the radius of the circle (r) and the max distance (h) that the chord reaches away from the edge of the circle. 

INSTRUCTIONS: Choose your preferred units and enter the following:

• (r) Radius of Circle
• (h) Depth of Chord

Arc Angle(θ): The angle of the arc segment is returned in radians.  However, this can be automatically converted to other angle units via the pull-down menu.

The Math / Science

The formula for Angle of a Circle Arc is as follows:

θ = 2 • cos^-1( (r-h)/r)

where:

• θ = angle of the circle defining the arc
• r = circle radius
• h = depth of chord

Circle Calculators

• Circle Area -  Computes the area of a circle given the radius (A = π r²).
• Area of Circle Arc Segment f(r,θ) - Computes the area of an arc segment of a circle given the radius (r) and angle (θ)
• Area of Circle Arc Segment Area f(r,h) - Computes the area of an arc segment of a circle given radius (r) and the depth (h) into the circle.
• Area of Circle Sector f(r,Θ) - Computes the area of a sector (pie slice) of a circle given the radius (r) and angle (Θ).
• Angle of Circle Sector f(r,h) - Computes the angle in a circle from the radius and depth of the chord.
• Area of Circle Annulus - Computes the area of an annulus (ring) given the inner radius (r) and outer radius (R).
• Radius of Circle from Center and a Point - Computes the radius of a circle given the center point (h,k) and any other point (x,y) on the circle.
• Circumference of Circle -  Computes the circumference of a circle given the radius (C = 2 π r).
• Circle Arc Length - Computes the length of an arc length on a circle given the radius (r) and angle (Θ)
• Circle within a Triangle - Computes the radius of a circle inscribed within a triangle given the length of the three sides (a,b,c) of the triangle.
• Circle around a Triangle - Computes the radius of a circle that circumscribes a triangle given the length of the three sides (a,b,c) of the triangle.
• Circle Diameter from Area - Computes the radius and diameter of a circle from the area. 
• Circle Radius from Circumference - Computes the radius of a circle given the circumference.
• Circle Circumference from Area - Computes the circumference of a circle given the area.
• Circle Radius from Area - Computes the radius of a circle given the area.
• Chord Length: Computes the length of a chord in a circle from the radius and height.
• Chord Length from Arc Length and Radius: Computes the length of a chord on a circle based on the circle's radius (r) and the length of the arc (a).
• Circle Radius from Chord - Computes the radius of a circle based on the length of a chord and the chord's center height.
• Circle Equation from Center and one Point - Develops the general equation of a circle based on the coordinates of the center (h,k) and any point on the circle (x,y).
• Circle Equation from Three Points: Develops the general equation of a circle that goes through three points that are not in a straight line.
• Circle with same Perimeter as an Ellipse - Computes the radius of the circle with the same perimeter of an ellipse defined by the semi-major and semi-minor axes.
• Rectangles to Cover a Circle - Computes the number of rectangles needed to minimally cover a circle based on the circle's diameter and the length and width of the rectangles.