`V_f = sqrt( V_i ^2+2* a *( x_f - x_i ))`

Enter a value for all fields

The Final Velocity calculator computes the final velocity based on an initial velocity, distance traveled between two points and a constant acceleration.

INSTRUCTIONS: Choose units and enter the following:

• (V_i) Initial Velocity
• (a) Acceleration
• (x_f) Final Displacement
• (x_i) Initial Displacement

Final Velocity (V_f): The velocity is returned in meters per second.  However, this can be automatically converted to compatible units via the pull-down men.

The Math / Science

The final velocity equation computes the square of the final velocity that a body would achieve after traveling in a straight line some distance at constant acceleration. This an illustrative step in calculating the actual `v_f` based on acceleration and time.  See the derivation below.

The formula for the final velocity is:

`V_f = sqrt(V_i^2+2*a*(x_f-x_i))`

where:

• V_f = Final Velocity
• x_i = initial displacement
• x_f = final displacement
• a = constant acceleration
• V_i = initial velocity

DERIVATION

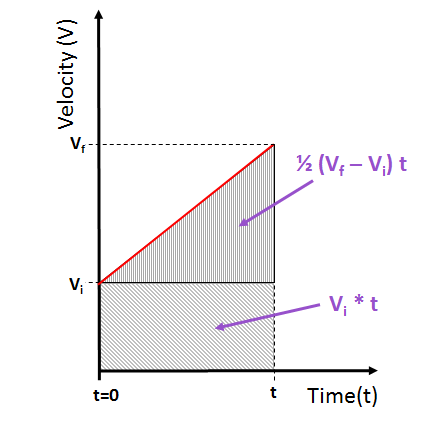
Since acceleration is constant, we know that the final velocity is the sum of the initial velocity and the velocity increase due to the acceleration.  In other words:

[1] `V_f = V_i + a *  t`

We also know that the distance traveled, d, is the sum of the distance the object would travel at its starting velocity, `V_i`, plus the distance it would travel while increasing velocity from `V_i` to `V_f`:

[2] `D = (V_i * t) + (1/2 * (V_f - V_i) * t)`

[3] `D = t * (V_i + 1/2 * V_f  -  1/2 * V_i)`

[4] `D = t * 1/2 (V_i + V_f)`

[5]    `=>   t = (2 * D) / (V_i + V_f)`

Substituting [5} into [1]:

[6] `V_f   =  V_i + a *  ((2 * D) / (V_i + V_f))`

Multiplying both sides by '(V_i + V_f)`:

[7] `V_i *V_f + V_f^2  = V_i^2 + V_i * V_f + 2*A*D`

Cancelling term `V_i* V_f`:

[8] `V_f^2 = V_i^2 + 2*a*D`,   where `D = x_f - x_0`

[9] `V_f^2 = V_i^2 + 2*a*(x_f - x_0)`

This equation [9] computes the resultant `V_f^2`, which is not useful in most cases, so we want to get the square root of this resultant:

[10] `V_f = sqrt(V_i^2 + 2*a*(x_f - x_0))`

EXTERNAL LINKS

Khan Academy's Average velocity for constant acceleration