35.3 Bound states by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

35.3 Bound states

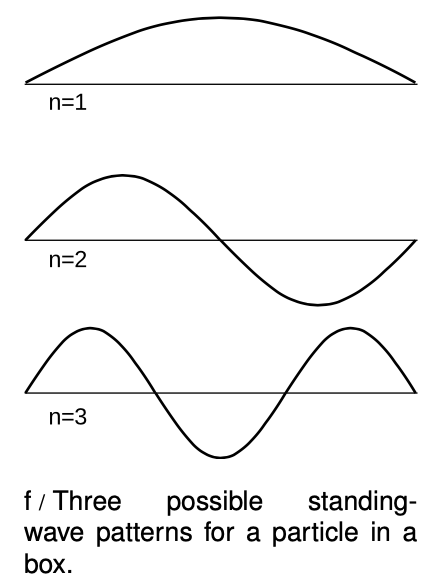Electrons are at their most interesting when they're in atoms, that is, when they are bound within a small region of space. We can understand a great deal about atoms and molecules based on simple arguments about such bound states, without going into any of the realistic details of atom. The simplest model of a bound state is known as the particle in a box: like a ball on a pool table, the electron feels zero force while in the interior, but when it reaches an edge it encounters a wall that pushes back inward on it with a large force. In particle language, we would describe the electron as bouncing off of the wall, but this incorrectly assumes that the electron has a certain path through space. It is more correct to describe the electron as a wave that undergoes `100%` reflection at the boundaries of the box.

Like a generation of physics students before me, I rolled my eyes when initially introduced to the unrealistic idea of putting a particle in a box. It seemed completely impractical, an artificial textbook invention. Today, however, it has become routine to study electrons in rectangular boxes in actual laboratory experiments. The “box” is actually just an empty cavity within a solid piece of silicon, amounting in volume to a few hundred atoms. The methods for creating these electron-in-a-box setups (known as “quantum dots”) were a by-product of the development of technologies for fabricating computer chips.

For simplicity let's imagine a one-dimensional electron in a box, i.e., we assume that the electron is only free to move along a line. The resulting standing wave patterns, of which the first three are shown in figure f, are just like some of the patterns we encountered with sound waves in musical instruments. The wave patterns must be zero at the ends of the box, because we are assuming the walls are impenetrable, and there should therefore be zero probability of finding the electron outside the box. Each wave pattern is labeled according to nn, the number of peaks and valleys it has. In quantum physics, these wave patterns are referred to as “states” of the particle-in-the-box system.

The following seemingly innocuous observations about the particle in the box lead us directly to the solutions to some of the most vexing failures of classical physics:

The particle's energy is quantized (can only have certain values).Each wavelength corresponds to a certain momentum, and a given momentum implies a definite kinetic energy, `E=p^2"/"(2m)`. (This is the second type of energy quantization we have encountered. The type we studied previously had to do with restricting the number of particles to a whole number, while assuming some specific wavelength and energy for each particle. This type of quantization refers to the energies that a single particle can have. Both photons and matter particles demonstrate both types of quantization under the appropriate circumstances.)

The particle has a minimum kinetic energy. Long wavelengths correspond to low momenta and low energies. There can be no state with an energy lower than that of the n=1n1 state, called the ground state.

The smaller the space in which the particle is confined, the higher its kinetic energy must be. Again, this is because long wavelengths give lower energies.

Example 3: Spectra of thin gases

A fact that was inexplicable by classical physics was that thin gases absorb and emit light only at certain wavelengths. This was observed both in earthbound laboratories and in the spectra of stars. Figure g shows the example of the spectrum of the star Sirius, in which there are “gap teeth” at certain wavelengths. Taking this spectrum as an example, we can give a straightforward explanation using quantum physics.

Energy is released in the dense interior of the star, but the outer layers of the star are thin, so the atoms are far apart and electrons are confined within individual atoms. Although their standing-wave patterns are not as simple as those of the particle in the box, their energies are quantized.

When a photon is on its way out through the outer layers, it can be absorbed by an electron in an atom, but only if the amount of energy it carries happens to be the right amount to kick the electron from one of the allowed energy levels to one of the higher levels. The photon energies that are missing from the spectrum are the ones that equal the difference in energy between two electron energy levels. (The most prominent of the absorption lines in Sirius's spectrum are absorption lines of the hydrogen atom.)

Example 4: The stability of atoms

In many Star Trek episodes the Enterprise, in orbit around a planet, suddenly lost engine power and began spiraling down toward the planet's surface. This was utter nonsense, of course, due to conservation of energy: the ship had no way of getting rid of energy, so it did not need the engines to replenish it.

Consider, however, the electron in an atom as it orbits the nucleus. The electron does have a way to release energy: it has an acceleration due to its continuously changing direction of motion, and according to classical physics, any accelerating charged particle emits electromagnetic waves. According to classical physics, atoms should collapse!

The solution lies in the observation that a bound state has a minimum energy. An electron in one of the higher-energy atomic states can and does emit photons and hop down step by step in energy. But once it is in the ground state, it cannot emit a photon because there is no lower-energy state for it to go to.

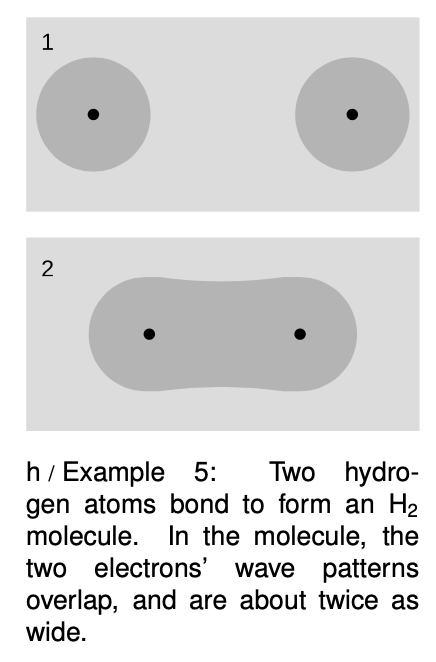Example 5: Chemical bonds in hydrogen molecules

I began this chapter with a classical argument that chemical bonds, as in an `H_2` molecule, should not exist. Quantum physics explains why this type of bonding does in fact occur. When the atoms are next to each other, the electrons are shared between them. The “box” is about twice as wide, and a larger box allows a smaller energy. Energy is required in order to separate the atoms. (A qualitatively different type of bonding is discussed in on page 997.)

Discussion Questions

A   Neutrons attract each other via the strong nuclear force, so according to classical physics it should be possible to form nuclei out of clusters of two or more neutrons, with no protons at all. Experimental searches, however, have failed to turn up evidence of a stable two-neutron system (dineutron) or larger stable clusters. These systems are apparently not just unstable in the sense of being able to beta decay but unstable in the sense that they don't hold together at all. Explain based on quantum physics why a dineutron might spontaneously fly apart.

B   The following table shows the energy gap between the ground state and the first excited state for four nuclei, in units of picojoules. (The nuclei were chosen to be ones that have similar structures, e.g., they are all spherical in shape.)

nucleus	energy gap (picojoules)
4He	3.234
16O	0.968
40Ca	0.536
208Pb	0.418

Explain the trend in the data.

35.3 Bound states by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.