24.5 Electromagnetic waves by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

24.5 Electromagnetic waves

The most important consequence of induction is the existence of electromagnetic waves. Whereas a gravitational wave would consist of nothing more than a rippling of gravitational fields, the principle of induction tells us that there can be no purely electrical or purely magnetic waves. Instead, we have waves in which there are both electric and magnetic fields, such as the sinusoidal one shown in the figure. Maxwell proved that such waves were a direct consequence of his equations, and derived their properties mathematically. The derivation would be beyond the mathematical level of this book, so we will just state the results.

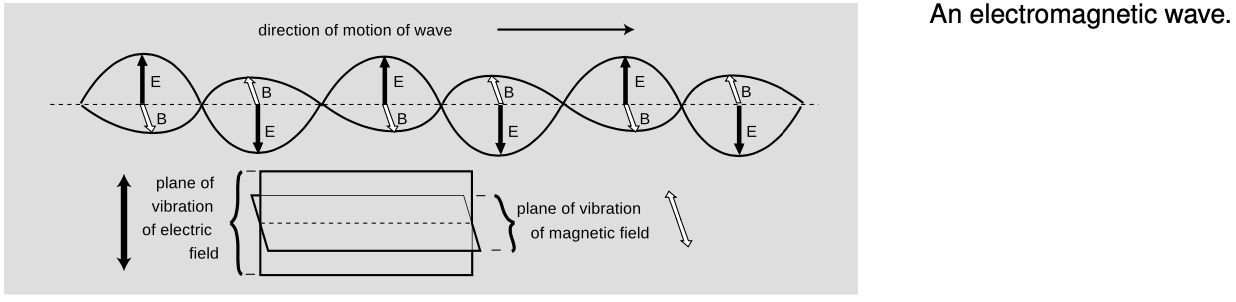
A sinusoidal electromagnetic wave has the geometry shown above. The `E` and `B` fields are perpendicular to the direction of motion, and are also perpendicular to each other. If you look along the direction of motion of the wave, the `B` vector is always 90 degrees clockwise from the `E` vector. In a plane wave, the magnitudes of the two fields are related by `|E|=c|B|`.

How is an electromagnetic wave created? It could be emitted, for example, by an electron orbiting an atom or currents going back and forth in a transmitting antenna. In general any accelerating charge will create an electromagnetic wave, although only a current that varies sinusoidally with time will create a sinusoidal wave. Once created, the wave spreads out through space without any need for charges or currents along the way to keep it going. As the electric field oscillates back and forth, it induces the magnetic field, and the oscillating magnetic field in turn creates the electric field. The whole wave pattern propagates through empty space at the velocity `c`.

Example 7: Einstein's motorcycle

As a teenage physics student, Einstein imagined the following paradox. (See p. 501.) What if he could get on a motorcycle and ride at speed `c`, alongside a beam of light? In his frame of reference, he observes constant electric and magnetic fields. But only a changing electric field can induce a magnetic field, and only a changing magnetic field can induce an electric field. The laws of physics are violated in his frame, and this seems to violate the principle that all frames of reference are equally valid.

The resolution of the paradox is that `c` is a universal speed limit, so the motorcycle can't be accelerated to `c`. Observers can never be at rest relative to a light wave, so no observer can have a frame of reference in which a light wave is observed to be at rest.

Example 8: Reflection

The wave in figure q hits a silvered mirror. The metal is a good conductor, so it has constant voltage throughout, and the electric field equals zero inside it: the wave doesn't penetrate and is `100%` reflected. If the electric field is to be zero at the surface as well, the reflected wave must have its electric field inverted (p. 513), so that the incident and reflected fields cancel there.

But the magnetic field of the reflected wave is not inverted. This is because the reflected wave, when viewed along its leftward direction of propagation, needs to have its `B` vector `90` degrees clockwise from its `E` vector.

Polarization

Two electromagnetic waves traveling in the same direction through space can differ by having their electric and magnetic fields in different directions, a property of the wave called its polarization.

Light is an electromagnetic wave

Once Maxwell had derived the existence of electromagnetic waves, he became certain that they were the same phenomenon as light. Both are transverse waves (i.e., the vibration is perpendicular to the direction the wave is moving), and the velocity is the same.

Heinrich Hertz (for whom the unit of frequency is named) verified Maxwell's ideas experimentally. Hertz was the first to succeed in producing, detecting, and studying electromagnetic waves in detail using antennas and electric circuits. To produce the waves, he had to make electric currents oscillate very rapidly in a circuit. In fact, there was really no hope of making the current reverse directions at the frequencies of `10^15` Hz possessed by visible light. The fastest electrical oscillations he could produce were `10^9` Hz, which would give a wavelength of about `30` cm. He succeeded in showing that, just like light, the waves he produced were polarizable, and could be reflected and refracted (i.e., bent, as by a lens), and he built devices such as parabolic mirrors that worked according to the same optical principles as those employing light. Hertz's results were convincing evidence that light and electromagnetic waves were one and the same.

The electromagnetic spectrum

Today, electromagnetic waves with frequencies in the range employed by Hertz are known as radio waves. Any remaining doubts that the “Hertzian waves,” as they were then called, were the same type of wave as light waves were soon dispelled by experiments in the whole range of frequencies in between, as well as the frequencies outside that range. In analogy to the spectrum of visible light, we speak of the entire electromagnetic spectrum, of which the visible spectrum is one segment.

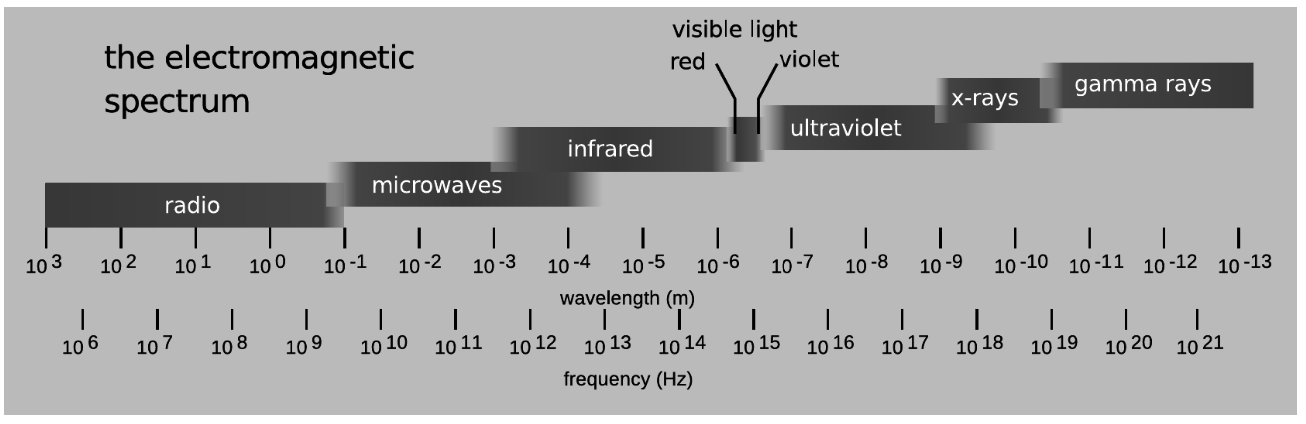
The terminology for the various parts of the spectrum is worth memorizing, and is most easily learned by recognizing the logical relationships between the wavelengths and the properties of the waves with which you are already familiar. Radio waves have wavelengths that are comparable to the size of a radio antenna, i.e., meters to tens of meters. Microwaves were named that because they have much shorter wavelengths than radio waves; when food heats unevenly in a microwave oven, the small distances between neighboring hot and cold spots is half of one wavelength of the standing wave the oven creates. The infrared, visible, and ultraviolet obviously have much shorter wavelengths, because otherwise the wave nature of light would have been as obvious to humans as the wave nature of ocean waves. To remember that ultraviolet, x-rays, and gamma rays all lie on the short-wavelength side of visible, recall that all three of these can cause cancer. (As we'll discuss later in the course, there is a basic physical reason why the cancer-causing disruption of DNA can only be caused by very short-wavelength electromagnetic waves. Contrary to popular belief, microwaves cannot cause cancer, which is why we have microwave ovens and not x-ray ovens!)

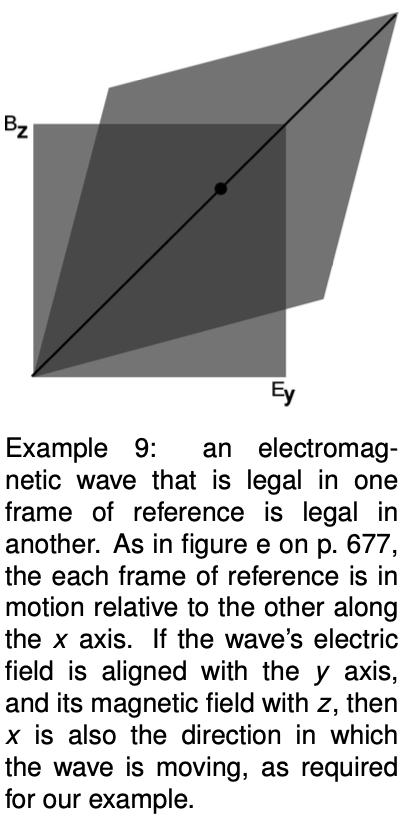Example 9: Switching frames of reference

If we switch to a different frame of reference, a legal light wave should still be legal. Consider the requirement `E=cB`, in the case where observer 1 says observer 2 is trying to run away from the wave. In figure e on p. 677, we saw that the familiar parallelogram graphs described the transformation of electric and magnetic fields from one frame of reference to another. These pictures are intended to be used in units where `c=1`, so the requirement for the fields becomes `E=B`, and such a combination of fields is represented by a dot on the diagonal, which is the same line in both frames.

Example 10: Why the sky is blue

When sunlight enters the upper atmosphere, a particular air molecule finds itself being washed over by an electromagnetic wave of frequency `f`. The molecule's charged particles (nuclei and electrons) act like oscillators being driven by an oscillating force, and respond by vibrating at the same frequency `f`. Energy is sucked out of the incoming beam of sunlight and converted into the kinetic energy of the oscillating particles. However, these particles are accelerating, so they act like little radio antennas that put the energy back out as spherical waves of light that spread out in all directions. An object oscillating at a frequency `f` has an acceleration proportional to `f^2`, and an accelerating charged particle creates an electromagnetic wave whose fields are proportional to its acceleration, so the field of the reradiated spherical wave is proportional to `f^2`. The energy of a field is proportional to the square of the field, so the energy of the reradiated wave is proportional to `f^4`. Since blue light has about twice the frequency of red light, this process is about `2^4=16` times as strong for blue as for red, and that's why the sky is blue.

Momentum of light

Newton defined momentum as `mv`, which would imply that light, which has no mass, should have no momentum. But Newton's laws only work at speeds small compared to the speed of light, and light travels at the speed of light. In fact, it's straightforward to show that electromagnetic waves have momentum. If a light wave strikes an ohmic surface, as in figure r, the wave's electric field causes charges to vibrate back and forth in the surface. These currents then experience a magnetic force from the wave's magnetic field, and application of the geometrical rule on p. 680 shows that the resulting force is in the direction of propagation of the wave. A light wave has momentum and inertia. This is explored further in problem 12 on p. 789. Figure s shows an experimental confirmation.

24.5 Electromagnetic waves by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.