LM 33.4 Exponential decay and half-life Collection
33.4 Exponential decay and half-life by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
33.4 Exponential decay and half-life
Most people know that radioactivity “lasts a certain amount of time,” but that simple statement leaves out a lot. As an example, consider the following medical procedure used to diagnose thyroid function. A very small quantity of the isotope 131I, produced in a nuclear reactor, is fed to or injected into the patient. The body's biochemical systems treat this artificial, radioactive isotope exactly the same as 127I, which is the only naturally occurring type. (Nutritionally, iodine is a necessary trace element. Iodine taken into the body is partly excreted, but the rest becomes concentrated in the thyroid gland. Iodized salt has had iodine added to it to prevent the nutritional deficiency known as goiters, in which the iodine-starved thyroid becomes swollen.) As the 131I undergoes beta decay, it emits electrons, neutrinos, and gamma rays. The gamma rays can be measured by a detector passed over the patient's body. As the radioactive iodine becomes concentrated in the thyroid, the amount of gamma radiation coming from the thyroid becomes greater, and that emitted by the rest of the body is reduced. The rate at which the iodine concentrates in the thyroid tells the doctor about the health of the thyroid.
If you ever undergo this procedure, someone will presumably explain a little about radioactivity to you, to allay your fears that you will turn into the Incredible Hulk, or that your next child will have an unusual number of limbs. Since iodine stays in your thyroid for a long time once it gets there, one thing you'll want to know is whether your thyroid is going to become radioactive forever. They may just tell you that the radioactivity “only lasts a certain amount of time,” but we can now carry out a quantitative derivation of how the radioactivity really will die out.
Let Psurv(t) be the probability that an iodine atom will survive without decaying for a period of at least t. It has been experimentally measured that half all 131I atoms decay in 8 hours, so we have
Psurv(8hr)=0.5.
Now using the law of independent probabilities, the probability of surviving for 16 hours equals the probability of surviving for the first 8 hours multiplied by the probability of surviving for the second 8 hours,
Psurv(16hr)=0.50×0.50
=0.25.
Similarly we have
Psurv(24hr)=0.50×0.5×0.5
=0.125.
Generalizing from this pattern, the probability of surviving for any time t that is a multiple of 8 hours is
Psurv(t)=0.5t/8hr.
We now know how to find the probability of survival at intervals of 8 hours, but what about the points in time in between? What would be the probability of surviving for 4 hours? Well, using the law of independent probabilities again, we have
Psurv(8hr)=Psurv(4hr)×Psurv(4hr),
which can be rearranged to give
Psurv(4hr)=√Psurv(8hr)
=√0.5
=0.707.
This is exactly what we would have found simply by plugging in Psurv(t)=0.5t/8hr and ignoring the restriction to multiples of 8 hours. Since 8 hours is the amount of time required for half of the atoms to decay, it is known as the half-life, written t1/2 . The general rule is as follows:
{exponential decay equation}
Psurv(t)=0.5t/t1/2
Using the rule for calculating averages, we can also find the number of atoms, N(t), remaining in a sample at time t:
N(t)=N(0)×0.5t/t1/2
Both of these equations have graphs that look like dying-out exponentials, as in the example below.
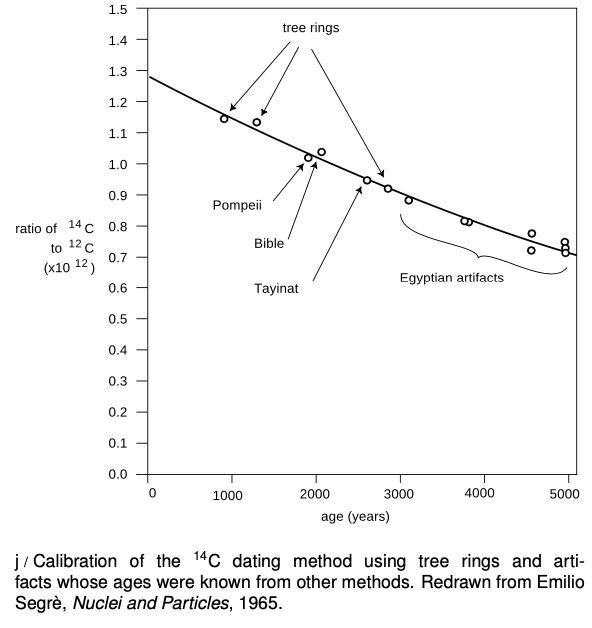
Example 2: 14C Dating
Almost all the carbon on Earth is 12C,but not quite.The isotope 14C, with a half-life of 5600 years, is produced by cosmic rays in the atmosphere. It decays naturally, but is replenished at such a rate that the fraction of 14C in the atmosphere remains constant, at 1.3×10-12. Living plants and animals take in both 12Cand 14C from the atmosphere and incorporate both into their bodies. Once the living organism dies, it no longer takes in C atoms from the atmosphere, gradually falls off as it undergoes radioactive decay. This effect can be used to find the age of dead organisms, or human artifacts made from plants or animals. Figure j shows the exponential decay curve of 14C in various objects. Similar methods, using longer-lived isotopes, prove the earth was billions of years old, not a few thousand as some had claimed on religious grounds.
Example 3: Radioactive contamination at Chernobyl
⇒ One of the most dangerous radioactive isotopes released by the Chernobyl disaster in 1986 was 90Sr, whose half-life is 28 years. (a) How long will it be before the contamination is reduced to one tenth of its original level? (b) If a total of 1027 atoms was released, about how long would it be before not a single atom was left?
⇒ (a) We want to know the amount of time that a 90Sr, nucleus has a probability of 0.1 of surviving. Starting with the exponential decay formula,
Psurv=0.5t/t1/2
we want to solve for t. Taking natural logarithms of both sides,
lnP=tt1/2ln0.5,
so
t=t1/2ln0.5lnP
Plugging in P=0.1 and t1/2=28 years, we get t=93 years.
(b) This is just like the first part, but P=10-27 . The result is about 2500 years.
Rate of decay
If you want to find how many radioactive decays occur within a time interval lasting from time t to time t+Δt, the most straightforward approach is to calculate it like this:
(number of decays between t and t+Δt)
=N(t)-N(t+Δt)
=N(0)[Psurv(t)-Psurv(t+Δt)]
=N(0)[0.5t/t1/2-0.5(t+Δt)/t1/2]
=N(0)[1-0.5Δt/t1/2]0.5t/t1/2
A problem arises when Δt is small compared to t1/2. For instance, suppose you have a hunk of 1022 atoms of 235U, with a half-life of 700 million years, which is 2.2×1016s. You want to know how many decays will occur in Δt=1s. Since we're specifying the current number of atoms, t=0. As you plug in to the formula above on your calculator, the quantity 0.5Δt/t1/2 comes out on your calculator to equal one, so the final result is zero. That's incorrect, though. In reality, 0.5Δt/t1/2 should equal 0.999999999999999968, but your calculator only gives eight digits of precision, so it rounded it off to one. In other words, the probability that a 235U atom will survive for 1s is very close to one, but not equal to one. The number of decays in one second is therefore 3.2×105, not zero.
Well, my calculator only does eight digits of precision, just like yours, so how did I know the right answer? The way to do it is to use the following approximation:
ab≈1+blna, ifb≪1
(The symbol ≪ means “is much less than.”) Using it, we can find the following approximation:
(number of decays between t and t+Deltat)
=N(0)[1-0.5(Δt)/t1/2]0.5t/t1/2
≈N(0)[1-(1+Δtt1/2ln0.5)]0.5t/t1/2
≈(ln2)N(0)0.5t/t1/2Δtt1/2
This also gives us a way to calculate the rate of decay, i.e., the number of decays per unit time. Dividing by Δt on both sides, we have
(decays per unit time)≈
ln2N(0)t1/20.5t/t1/2,if Δt≪t1/2.
Example 4: The hot potato
⇒ A nuclear physicist with a demented sense of humor tosses you a cigar box, yelling “hot potato.” The label on the box says “contains 1020 atoms of 17F, half-life of 66 s, produced today in our reactor at 1 p.m.” It takes you two seconds to read the label, after which you toss it behind some lead bricks and run away. The time is 1:40 p.m. Will you die?
⇒ The time elapsed since the radioactive fluorine was produced in the reactor was 40 minutes, or 2400 s. The number of elapsed half-lives is therefore t/(t1/2)=36. The initial number of atoms was N(0)=1020 . The number of decays per second is now about 107s-1, so it produced about 2×107 high-energy electrons while you held it in your hands. Although twenty million electrons sounds like a lot, it is not really enough to be dangerous.
By the way, none of the equations we've derived so far was the actual probability distribution for the time at which a particular radioactive atom will decay. That probability distribution would be found by substituting N(0)=1 into the equation for the rate of decay.
If the sheer number of equations is starting to seem formidable, let's pause and think for a second. The simple equation for Psurv is something you can derive easily from the law of independent probabilities any time you need it. From that, you can quickly find the exact equation for the rate of decay. The derivation of the approximate equations for Δt≪t is a little hairier, but note that except for the factors of ln2, everything in these equations can be found simply from considerations of logic and units. For instance, a longer half-life will obviously lead to a slower rate of decays, so it makes sense that we divide by it. As for the ln2 factors, they are exactly the kind of thing that one looks up in a book when one needs to know them.
Discussion Questions
A In the medical procedure involving 131I, why is it the gamma rays that are detected, not the electrons or neutrinos that are also emitted?
B For 1 s, Fred holds in his hands 1 kg of radioactive stuff with a half-life of 1000 years. Ginger holds 1 kg of a different substance, with a half-life of 1 min, for the same amount of time. Did they place themselves in equal danger, or not?
C How would you interpret it if you calculated N(t), and found it was less than one?
D Does the half-life depend on how much of the substance you have? Does the expected time until the sample decays completely depend on how much of the substance you have?
33.4 Exponential decay and half-life by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Calculators and Collections
- Comments
- Attachments
- Stats
No comments |
