4.1 Force by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
4.1 Force
We need only explain changes in motion, not motion itself.
So far you've studied the measurement of motion in some detail, but not the reasons why a certain object would move in a certain way. This chapter deals with the “why” questions. Aristotle's ideas about the causes of motion were completely wrong, just like all his other ideas about physical science, but it will be instructive to start with them, because they amount to a road map of modern students' incorrect preconceptions.
Aristotle thought he needed to explain both why motion occurs and why motion might change. Newton inherited from Galileo the important counter-Aristotelian idea that motion needs no explanation, that it is onlychanges in motion that require a physical cause. Aristotle's needlessly complex system gave three reasons for motion:
Natural motion, such as falling, came from the tendency of objects to go to their “natural” place, on the ground, and come to rest.
Voluntary motion was the type of motion exhibited by animals, which moved because they chose to.
Forced motion occurred when an object was acted on by some other object that made it move.
Motion changes due to an interaction between two objects.
In the Aristotelian theory, natural motion and voluntary motion are one-sided phenomena: the object causes its own motion. Forced motion is supposed to be a two-sided phenomenon, because one object imposes its “commands” on another. Where Aristotle conceived of some of the phenomena of motion as one-sided and others as two-sided, Newton realized that a change in motion was always a two-sided relationship of a
force acting between two physical objects.
The one-sided “natural motion” description of falling makes a crucial omission. The acceleration of a falling object is not caused by its own “natural” tendencies but by an attractive force between it and the planet Earth. Moon rocks brought back to our planet do not “want” to fly back up to the moon because the moon is their “natural” place. They fall to the floor when you drop them, just like our homegrown rocks. As we'll discuss in more detail later in this course, gravitational forces are simply an attraction that occurs between any two physical objects. Minute gravitational forces can even be measured between human-scale objects in the laboratory.
The idea of natural motion also explains incorrectly why things come to rest. A basketball rolling across a beach slows to a stop because it is interacting with the sand via a frictional force, not because of its own desire to be at rest. If it was on a frictionless surface, it would never slow down. Many of Aristotle's mistakes stemmed from his failure to recognize friction as a force.
The concept of voluntary motion is equally flawed. You may have been a little uneasy about it from the start, because it assumes a clear distinction between living and nonliving things. Today, however, we are used to having the human body likened to a complex machine. In the modern world-view, the border between the living and the inanimate is a fuzzy no-man's land inhabited by viruses, prions, and silicon chips. Furthermore, Aristotle's statement that you can take a step forward “because you choose to” inappropriately mixes two levels of explanation. At the physical level of explanation, the reason your body steps forward is because of a frictional force acting between your foot and the floor. If the floor was covered with a puddle of oil, no amount of “choosing to” would enable you to take a graceful stride forward.
Forces can all be measured on the same numerical scale.
In the Aristotelian-scholastic tradition, the description of motion as natural, voluntary, or forced was only the broadest level of classification, like splitting animals into birds, reptiles, mammals, and amphibians. There might be thousands of types of motion, each of which would follow its own rules. Newton's realization that all changes in motion were caused by two-sided interactions made it seem that the phenomena might have more in common than had been apparent. In the Newtonian description, there is only one cause for a change in motion, which we call
force.
Forces may be of different types, but they all produce changes in motion according to the same rules. Any
acceleration that can be produced by a magnetic
force can equally well be produced by an appropriately controlled stream of water. We can speak of two
forces as being equal if they produce the same change in motion when applied in the same situation, which means that they pushed or pulled equally hard in the same direction.
The idea of a numerical scale of force and the newton unit were introduced in chapter 0. To recapitulate briefly, a force is when a pair of objects push or pull on each other, and one newton is the force required to accelerate a 1-kg object from rest to a speed of 1 m/s in 1 second.
More than one force on an object
As if we hadn't kicked poor Aristotle around sufficiently, his theory has another important flaw, which is important to discuss because it corresponds to an extremely common student misconception. Aristotle conceived of forced motion as a relationship in which one object was the boss and the other “followed orders.” It therefore would only make sense for an object to experience one
force at a time, because an object couldn't follow orders from two sources at once. In the Newtonian theory,
forces are numbers, not orders, and if more than one
force acts on an object at once, the result is found by adding up all the
forces. It is unfortunate that the use of the English word “force” has become standard, because to many people it suggests that you are “forcing” an object to do something. The force of the earth's gravity cannot “force” a boat to sink, because there are other
forces acting on the boat. Adding them up gives a total of zero, so the boat
accelerates neither up nor down.
Objects can exert forces on each other at a distance.
Aristotle declared that
forces could only act between objects that were touching, probably because he wished to avoid the type of occult speculation that attributed physical phenomena to the influence of a distant and invisible pantheon of gods. He was wrong, however, as you can observe when a magnet leaps onto your refrigerator or when the planet earth exerts
gravitational forces on objects that are in the air. Some types of
forces, such as
friction, only operate between objects in contact, and are called contact
forces. Magnetism, on the other hand, is an example of a noncontact
force. Although the magnetic
force gets stronger when the magnet is closer to your refrigerator, touching is not required.
Weight
In physics, an object's
weight, `FW`, is defined as the
earth's gravitational force on it. The SI unit of
weight is therefore the Newton. People commonly refer to the kilogram as a unit of weight, but the kilogram is a unit of mass, not weight. Note that an object's weight is not a fixed property of that object. Objects weigh more in some places than in others, depending on the local strength of gravity. It is their mass that always stays the same. A baseball pitcher who can throw a 90-mile-per-hour fastball on earth would not be able to throw any faster on the moon, because the ball's inertia would still be the same.
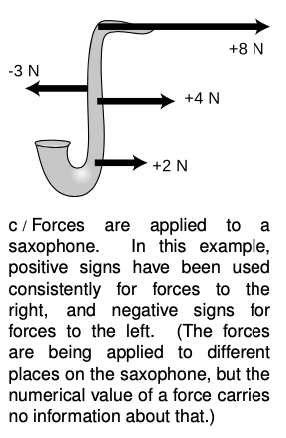Positive and negative signs of force
We'll start by considering only cases of one-dimensional center-of-mass motion in which all the
forces are parallel to the direction of motion, i.e., either directly forward or backward. In one dimension, plus and minus signs can be used to indicate directions of
forces, as shown in figure
c. We can then refer generically to addition of
forces, rather than having to speak sometimes of addition and sometimes of subtraction. We add the
forces shown in the figure and get 11 N. In general, we should choose a one-dimensional coordinate system with its `x` axis parallel the direction of motion.
Forces that point along the positive `x` axis are positive, and
forces in the opposite direction are negative.
Forces that are not directly along the `x` axis cannot be immediately incorporated into this scheme, but that's OK, because we're avoiding those cases for now.
Discussion Questions
A In chapter 0, I defined 1 N as the force that would accelerate a 1-kg mass from rest to 1 m/s in 1 s. Anticipating the following section, you might guess that 2 N could be defined as the force that would accelerate the same mass to twice the speed, or twice the mass to the same speed. Is there an easier way to define 2 N based on the definition of 1 N?
4.1 Force by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.