32.4 Huygens' principle by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

32.4 Huygens' principle

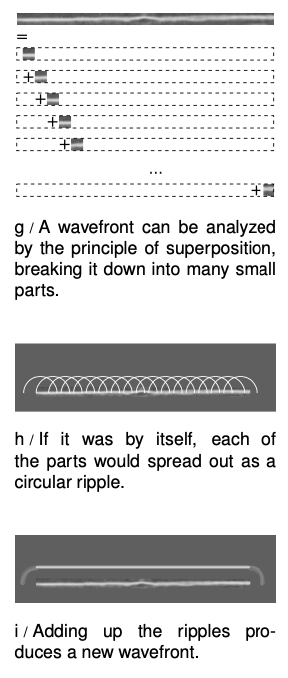
Returning to the example of double-slit diffraction, f, note the strong visual impression of two overlapping sets of concentric semicircles. This is an example of Huygens' principle, named after a Dutch physicist and astronomer. (The first syllable rhymes with “boy.”) Huygens' principle states that any wavefront can be broken down into many small side-by-side wave peaks, g, which then spread out as circular ripples, h, and by the principle of superposition, the result of adding up these sets of ripples must give the same result as allowing the wave to propagate forward, i. In the case of sound or light waves, which propagate in three dimensions, the “ripples” are actually spherical rather than circular, but we can often imagine things in two dimensions for simplicity.

In double-slit diffraction the application of Huygens' principle is visually convincing: it is as though all the sets of ripples have been blocked except for two. It is a rather surprising mathematical fact, however, that Huygens' principle gives the right result in the case of an unobstructed linear wave, h and i. A theoretically infinite number of circular wave patterns somehow conspire to add together and produce the simple linear wave motion with which we are familiar.

Since Huygens' principle is equivalent to the principle of superposition, and superposition is a property of waves, what Huygens had created was essentially the first wave theory of light. However, he imagined light as a series of pulses, like hand claps, rather than as a sinusoidal wave.

The history is interesting. Isaac Newton loved the atomic theory of matter so much that he searched enthusiastically for evidence that light was also made of tiny particles. The paths of his light particles would correspond to rays in our description; the only significant difference between a ray model and a particle model of light would occur if one could isolate individual particles and show that light had a “graininess” to it. Newton never did this, so although he thought of his model as a particle model, it is more accurate to say he was one of the builders of the ray model.

Almost all that was known about reflection and refraction of light could be interpreted equally well in terms of a particle model or a wave model, but Newton had one reason for strongly opposing Huygens' wave theory. Newton knew that waves exhibited diffraction, but diffraction of light is difficult to observe, so Newton believed that light did not exhibit diffraction, and therefore must not be a wave. Although Newton's criticisms were fair enough, the debate also took on the overtones of a nationalistic dispute between England and continental Europe, fueled by English resentment over Leibniz's supposed plagiarism of Newton's calculus. Newton wrote a book on optics, and his prestige and political prominence tended to discourage questioning of his model.

Thomas Young (1773-1829) was the person who finally, a hundred years later, did a careful search for wave interference effects with light and analyzed the results correctly. He observed double-slit diffraction of light as well as a variety of other diffraction effects, all of which showed that light exhibited wave interference effects, and that the wavelengths of visible light waves were extremely short. The crowning achievement was the demonstration by the experimentalist Heinrich Hertz and the theorist James Clerk Maxwell that light was an electromagnetic wave. Maxwell is said to have related his discovery to his wife one starry evening and told her that she was the only other person in the world who knew what starlight was.

32.4 Huygens' principle by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.