23.2 Magnetic interactions by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

23.2 Magnetic interactions

Think not that I am come to destroy the law, or the prophets: I am not come to destroy, but to fulfill. -- Matthew 5:17

At this stage, you understand roughly as much about the classification of interactions as physicists understood around the year 1800. There appear to be three fundamentally different types of interactions: gravitational, electrical, and magnetic. Many types of interactions that appear superficially to be distinct --- stickiness, chemical interactions, the energy an archer stores in a bow --- are really the same: they're manifestations of electrical interactions between atoms. Is there any way to shorten the list any further? The prospects seem dim at first. For instance, we find that if we rub a piece of fur on a rubber rod, the fur does not attract or repel a magnet. The fur has an electric field, and the magnet has a magnetic field. The two 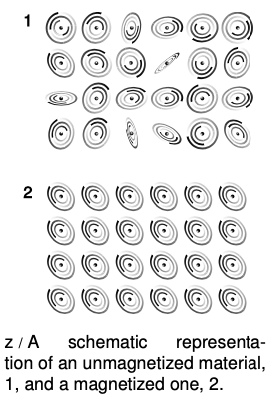are completely separate, and don't seem to affect one another. Likewise we can test whether magnetizing a piece of iron changes its weight. The weight doesn't seem to change by any measurable amount, so magnetism and gravity seem to be unrelated.

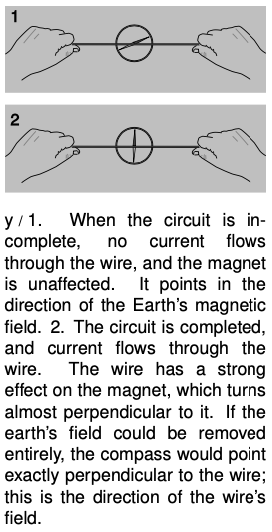
That was where things stood until 1820, when the Danish physicist Hans Christian Oersted was delivering a lecture at the University of Copenhagen, and he wanted to give his students a demonstration that would illustrate the cutting edge of research. He generated a current in a wire by making a short circuit across a battery, and held the wire near a magnetic compass. The ideas was to give an example of how one could search for a previously undiscovered link between electricity (the electric current in the wire) and magnetism. One never knows how much to believe from these dramatic legends, but the story is that the experiment he'd expected to turn out negative instead turned out positive: when he held the wire near the compass, the current in the wire caused the compass to twist!

People had tried similar experiments before, but only with static electricity, not with a moving electric current. For instance, they had hung batteries so that they were free to rotate in the earth's magnetic field, and found no effect; since the battery was not connected to a complete circuit, there was no current flowing. With Oersted's own setup, y, the effect was only produced when the “circuit was closed, but not when open, as certain very celebrated physicists in vain attempted several years ago.”

Oersted was eventually led to the conclusion that magnetism was an interaction between moving charges and other moving charges, i.e., between one current and another. A permanent magnet, he inferred, contained currents on a microscopic scale that simply weren't practical to measure with an ammeter. Today this seems natural to us, since we're accustomed to picturing an atom as a tiny solar system, with the electrons whizzing around the nucleus in circles. As shown in figure z, a magnetized piece of iron is different from an unmagnetized piece because the atoms in the unmagnetized piece are jumbled in random orientations, whereas the atoms in the magnetized piece are at least partially organized to face in a certain direction.

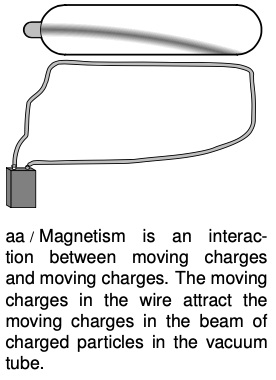Figure aa shows an example that is conceptually simple, but not very practical. If you try this with a typical vacuum tube, like a TV or computer monitor, the current in the wire probably won't be enough to produce a visible effect. A more practical method is to hold a magnet near the screen. We still have an interaction between moving charges and moving charges, but the swirling electrons in the atoms in the magnet are now playing the role played by the moving charges in the wire in figure aa. Warning: if you do this, make sure your monitor has a demagnetizing button! If not, then your monitor may be permanently ruined.
 

Relativity requires magnetism

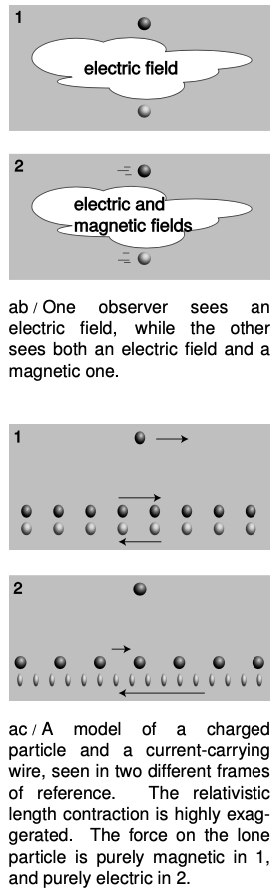
So magnetism is an interaction between moving charges and moving charges. But how can that be? Relativity tells us that motion is a matter of opinion. Consider figure ab. In this figure and in figure ac, the dark and light coloring of the particles represents the fact that one particle has positive charge and the other negative. Observer ab/2 sees the two particles as flying through space side by side, so they would interact both electrically (simply because they're charged) and magnetically (because they're charges in motion). But an observer moving along with them, ab/1, would say they were both at rest, and would expect only an electrical interaction. This seems like a paradox. Magnetism, however, comes not to destroy relativity but to fulfill it. Magnetic interactions must exist according to the theory of relativity. To understand how this can be, consider how time and space behave in relativity. Observers in different frames of reference disagree about the lengths of measuring sticks and the speeds of clocks, but the laws of physics are valid and self-consistent in either frame of reference. Similarly, observers in different frames of reference disagree about what electric and magnetic fields there are, but they agree about concrete physical events. An observer in frame of reference ab/1 says there are electric fields around the particles, and predicts that as time goes on, the particles will begin to accelerate towards one another, eventually colliding. She explains the collision as being due to the electrical attraction between the particles. A different observer, ab/2, says the particles are moving. This observer also predicts that the particles will collide, but explains their motion in terms of both an electric field and a magnetic field. As we'll see shortly, the magnetic field is required in order to maintain consistency between the predictions made in the two frames of reference.

To see how this really works out, we need to find a nice simple example. An example like figure ab is not easy to handle, because in the second frame of reference, the moving charges create fields that change over time at any given location, like when the V-shaped wake of a speedboat washes over a buoy. Examples like figure aa are easier, because there is a steady flow of charges, and all the fields stay the same over time. Figure ac/1 shows a simplified and idealized model of figure aa. The charge by itself is like one of the charged particles in the vacuum tube beam of figure aa, and instead of the wire, we have two long lines of charges moving in opposite directions. Note that, as discussed in discussion question C on page 575, the currents of the two lines of charges do not cancel out. The dark and light balls represent particles with opposite charges. Because of this, the total current in the “wire” is double what it would be if we took away one line.

As a model of figure aa, figure ac/1 is partly realistic and partly unrealistic. In a real piece of copper wire, there are indeed charged particles of both types, but it turns out that the particles of one type (the protons) are locked in place, while only some of the other type (the electrons) are free to move. The model also shows the particles moving in a simple and orderly way, like cars on a two-lane road, whereas in reality most of the particles are organized into copper atoms, and there is also a great deal of random thermal motion. The model's unrealistic features aren't a problem, because the point of this exercise is only to find one particular situation that shows magnetic effects must exist based on relativity.

What electrical force does the lone particle in figure ac/1 feel? Since the density of “traffic” on the two sides of the “road” is equal, there is zero overall electrical force on the lone particle. Each “car” that attracts the lone particle is paired with a partner on the other side of the road that repels it. If we didn't know about magnetism, we'd think this was the whole story: the lone particle feels no force at all from the wire.

Figure ac/2 shows what we'd see if we were observing all this from a frame of reference moving along with the lone charge. Here's where the relativity comes in. Relativity tells us that moving objects appear contracted to an observer who is not moving along with them. Both lines of charge are in motion in both frames of reference, but in frame 1 they were moving at equal speeds, so their contractions were equal. In frame 2, however, their speeds are unequal. The dark charges are moving more slowly than in frame 1, so in frame 2 they are less contracted. The light-colored charges are moving more quickly, so their contraction is greater now. The “cars” on the two sides of the “road” are no longer paired off, so the electrical forces on the lone particle no longer cancel out as they did in ac/1. The lone particle is attracted to the wire, because the particles attracting it are more dense than the ones repelling it. Furthermore, the attraction felt by the lone charge must be purely electrical, since the lone charge is at rest in this frame of reference, and magnetic effects occur only between moving charges and other moving charges.

Now observers in frames 1 and 2 disagree about many things, but they do agree on concrete events. Observer 2 is going to see the lone particle drift toward the wire due to the wire's electrical attraction, gradually speeding up, and eventually hit the wire. If 2 sees this collision, then 1 must as well. But 1 knows that the total electrical force on the lone particle is exactly zero. There must be some new type of force. She invents a name for this new type of force: magnetism. This was a particularly simple example, because the force was purely magnetic in one frame of reference, and purely electrical in another. In general, an observer in a certain frame of reference will measure a mixture of electric and magnetic fields, while an observer in another frame, in motion with respect to the first, says that the same volume of space contains a different mixture.

We therefore arrive at the conclusion that electric and magnetic phenomena aren't separate. They're different sides of the same coin. We refer to electric and magnetic interactions collectively as electromagnetic interactions. Our list of the fundamental interactions of nature now has two items on it instead of three: gravity and electromagnetism.

Oersted found that magnetism was an interaction between moving charges and other moving charges. We can see this in the situation described in figure ac/1, in which the result of the argument depended on the fact that both the lone charge and the charges in the wire were moving. To see this in a different way, we can apply the result of example 2 on p. 662, that for small velocities the `gamma` factor differs from 1 by about `v^2"/"2c^2`. Let the lone charge in figure ac/1 have velocity `u`, the ones in the wire `+/-v`. As we'll see on p. 682, velocities in relative motion don't exactly add and subtract relativistically, but as long as we assume that `u` and `v` are small, the correspondence principle guarantees that they will approximately add and subtract. Then the velocities in the lone charge's rest frame, ac/2, are approximately 0, `v-u`, and `-v-u`. The nonzero charge density of the wire in frame ac/2 is then proportional to the difference in the length contractions `gamma_(-v-u)-gamma_(v-u)approx2uv"/"c^2`. This depends on the product of the velocities `u` and `v`, which is as expected if magnetism is an interaction of moving charges with moving charges.

The basic rules for magnetic attractions and repulsions, shown in figure ad, aren't quite as simple as the ones for gravity and electricity. Rules ad/1 and ad/2 follow directly from our previous analysis of figure ac. Rules 3 and 4 are obtained by flipping the type of charge that the bottom particle has. For instance, rule 3 is like rule 1, except that the bottom charge is now the opposite type. This turns the attraction into a repulsion. (We know that flipping the charge reverses the interaction, because that's the way it works for electric forces, and magnetic forces are just electric forces viewed in a different frame of reference.)

Example 7: A magnetic weathervane placed near a current.

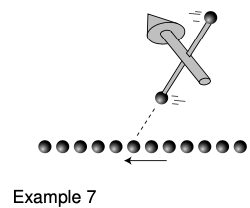Figure 23.2.1 shows a magnetic weathervane, consisting of two charges that spin in circles around the axis of the arrow. (The magnetic field doesn't cause them to spin; a motor is needed to get them to spin in the first place.) Just like the magnetic compass in figure y, the weathervane's arrow tends to align itself in the direction perpendicular to the wire. This is its preferred orientation because the charge close to the wire is attracted to the wire, while the charge far from the wire is repelled by it.

Discussion Question

A   Resolve the following paradox concerning the argument given in this section. We would expect that at any given time, electrons in a solid would be associated with protons in a definite way. For simplicity, let's imagine that the solid is made out of hydrogen (which actually does become a metal under conditions of very high pressure). A hydrogen atom consists of a single proton and a single electron. Even if the electrons are moving and forming an electric current, we would imagine that this would be like a game of musical chairs, with the protons as chairs and the electrons as people. Each electron has a proton that is its “friend,” at least for the moment. This is the situation shown in figure ac/1. How, then, can an observer in a different frame see the electrons and protons as not being paired up, as in ac/2?

23.2 Magnetic interactions by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.