34.4 Photons in three dimensions by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

34.4 Photons in three dimensions

Up until now I've been sneaky and avoided a full discussion of the three-dimensional aspects of the probability interpretation. The example of the carrot in the microwave oven, for example, reduced to a one-dimensional situation because we were considering three points along the same line and because we were only comparing ratios of probabilities. The purpose of bringing it up now is to head off any feeling that you've been cheated conceptually rather than to prepare you for mathematical problem solving in three dimensions, which would not be appropriate for the level of this course.

A typical example of a probability distribution in section 33.3 was the distribution of heights of human beings. The thing that varied randomly, height, `h`, had units of meters, and the probability distribution was a graph of a function `D(h)`. The units of the probability distribution had to be `m^(-1)`("inverse meters") so that areas under the curve, interpreted as probabilities, would be unitless: `("area")=('height")("width")=m^(-1)*m`.

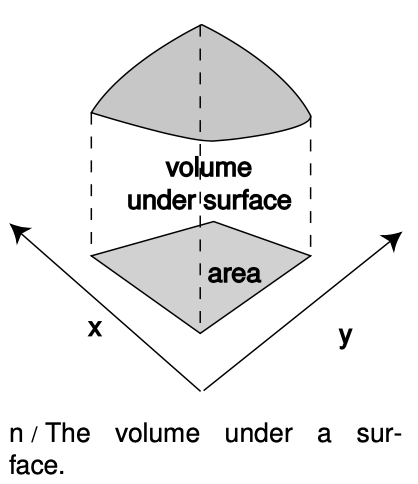Now suppose we have a two-dimensional problem, e.g., the probability distribution for the place on the surface of a digital camera chip where a photon will be detected. The point where it is detected would be described with two variables, `x` and `y`, each having units of meters. The probability distribution will be a function of both variables, `D(x,y)`. A probability is now visualized as the volume under the surface described by the function `D(x,y)`, as shown in figure n. The units of `D` must be `m^(-2)` so that probabilities will be unitless: `("probability")=("depth")("length")("width")=m^(-2)*m*m`.

Generalizing finally to three dimensions, we find by analogy that the probability distribution will be a function of all three coordinates, `D(x,y,z)`, and will have units of `m^(-3)`. It is, unfortunately, impossible to visualize the graph unless you are a mutant with a natural feel for life in four dimensions. If the probability distribution is nearly constant within a certain volume of space `v`, the probability that the photon is in that volume is simply `vD`. If you know enough calculus, it should be clear that this can be generalized to `P=intDdxdydz` if `D` is not constant.

34.4 Photons in three dimensions by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.