20.1 Reflection, transmission, and absorption by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
20.1 Reflection, transmission, and absorption
Reflection and transmission
Sound waves can echo back from a cliff, and light waves are reflected from the surface of a pond. We use the word reflection, normally applied only to light waves in ordinary speech, to describe any such case of a wave rebounding from a barrier. Figure b shows a circular water wave being reflected from a straight wall. In this chapter, we will concentrate mainly on reflection of waves that move in one dimension, as in figure c.
Wave reflection does not surprise us. After all, a material object such as a rubber ball would bounce back in the same way. But waves are not objects, and there are some surprises in store.
First, only part of the wave is usually reflected. Looking out through a window, we see light waves that passed through it, but a person standing outside would also be able to see her reflection in the glass. A light wave that strikes the glass is partly reflected and partly transmitted (passed) by the glass. The energy of the original wave is split between the two. This is different from the behavior of the rubber ball, which must go one way or the other, not both.
Second, consider what you see if you are swimming underwater and you look up at the surface. You see your own reflection. This is utterly counterintuitive, since we would expect the light waves to burst forth to freedom in the wide-open air. A material projectile shot up toward the surface would never rebound from the water-air boundary! Figure a shows a similar example.
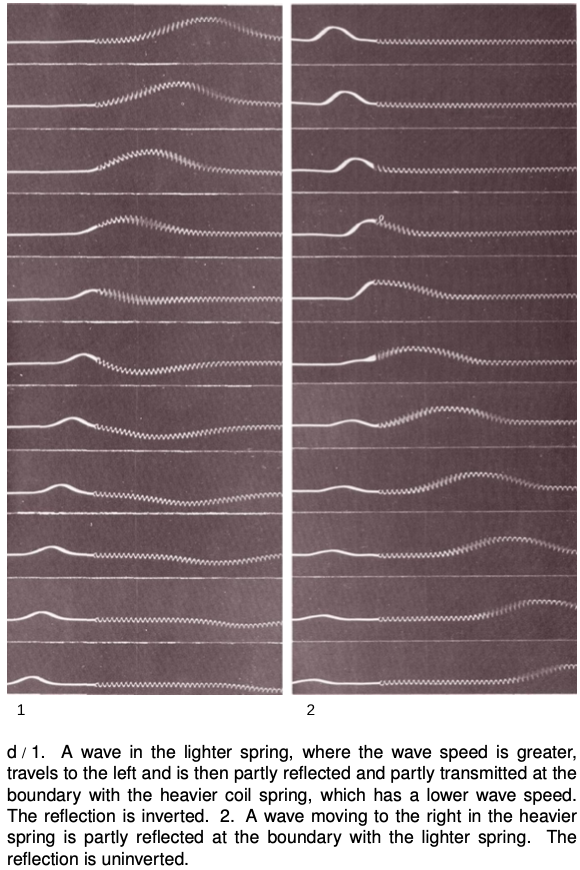
What is it about the difference between two media that causes waves to be partly reflected at the boundary between them? Is it their density? Their chemical composition? Ultimately all that matters is the speed of the wave in the two media. A wave is partially reflected and partially transmitted at the boundary between media in which it has different speeds. For example, the speed of light waves in window glass is about 30% less than in air, which explains why windows always make reflections. Figures d/1 and 2 show examples of wave pulses being reflected at the boundary between two coil springs of different weights, in which the wave speed is different.
Reflections such as b and c, where a wave encounters a massive fixed object, can usually be understood on the same basis as cases like d/1 and 2 later in this section, where two media meet. Example c, for instance, is like a more extreme version of example d/1. If the heavy coil spring in d/1 was made heavier and heavier, it would end up acting like the fixed wall to which the light spring in c has been attached.
self-check:
In figure c, the reflected pulse is upside-down, but its depth is just as big as the original pulse's height. How does the energy of the reflected pulse compare with that of the original?
(answer in the back of the PDF version of the book)
Example 1: Fish have internal ears.
Why don't fish have ear-holes? The speed of sound waves in a fish's body is not much different from their speed in water, so sound waves are not strongly reflected from a fish's skin. They pass right through its body, so fish can have internal ears.
Example 2: Whale songs traveling long distances
Sound waves travel at drastically different speeds through rock, water, and air. Whale songs are thus strongly reflected at both the bottom and the surface. The sound waves can travel hundreds of miles, bouncing repeatedly between the bottom and the surface, and still be detectable. Sadly, noise pollution from ships has nearly shut down this cetacean version of the internet.
Example 3: Long-distance radio communication.
Radio communication can occur between stations on opposite sides of the planet. The mechanism is similar to the one explained in example 2, but the three media involved are the earth, the atmosphere, and the ionosphere.
self-check:
Sonar is a method for ships and submarines to detect each other by producing sound waves and listening for echoes. What properties would an underwater object have to have in order to be invisible to sonar?
(answer in the back of the PDF version of the book)
The use of the word “reflection” naturally brings to mind the creation of an image by a mirror, but this might be confusing, because we do not normally refer to “reflection” when we look at surfaces that are not shiny. Nevertheless, reflection is how we see the surfaces of all objects, not just polished ones. When we look at a sidewalk, for example, we are actually seeing the reflecting of the sun from the concrete. The reason we don't see an image of the sun at our feet is simply that the rough surface blurs the image so drastically.
Inverted and uninverted reflections
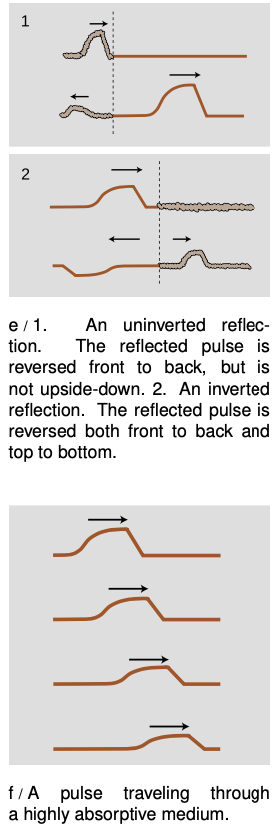
Notice how the pulse reflected back to the right in example d/1 comes back upside-down, whereas the one reflected back to the left in 2 returns in its original upright form. This is true for other waves as well. In general, there are two possible types of reflections, a reflection back into a faster medium and a reflection back into a slower medium. One type will always be an inverting reflection and one noninverting.
It's important to realize that when we discuss inverted and uninverted reflections on a string, we are talking about whether the wave is flipped across the direction of motion (i.e., upside-down in these drawings). The reflected pulse will always be reversed front to back, as shown in figure e. This is because it is traveling in the other direction. The leading edge of the pulse is what gets reflected first, so it is still ahead when it starts back to the left --- it's just that “ahead” is now in the opposite direction.
Absorption
So far we have tacitly assumed that wave energy remains as wave energy, and is not converted to any other form. If this was true, then the world would become more and more full of sound waves, which could never escape into the vacuum of outer space. In reality, any mechanical wave consists of a traveling pattern of vibrations of some physical medium, and vibrations of matter always produce heat, as when you bend a coat-hangar back and forth and it becomes hot. We can thus expect that in mechanical waves such as water waves, sound waves, or waves on a string, the wave energy will gradually be converted into heat. This is referred to as absorption.
The wave suffers a decrease in amplitude, as shown in figure f. The decrease in amplitude amounts to the same fractional change for each unit of distance covered. For example, if a wave decreases from amplitude 2 to amplitude 1 over a distance of 1 meter, then after traveling another meter it will have an amplitude of 1/2. That is, the reduction in amplitude is exponential. This can be proven as follows. By the principle of superposition, we know that a wave of amplitude 2 must behave like the superposition of two identical waves of amplitude 1. If a single amplitude-1 wave would die down to amplitude 1/2 over a certain distance, then two amplitude-1 waves superposed on top of one another to make amplitude `1+1=2` must die down to amplitude `1"/"2+1"/"2=1` over the same distance.
self-check:
As a wave undergoes absorption, it loses energy. Does this mean that it slows down?
(answer in the back of the PDF version of the book)
In many cases, this frictional heating effect is quite weak. Sound waves in air, for instance, dissipate into heat extremely slowly, and the sound of church music in a cathedral may reverberate for as much as 3 or 4 seconds before it becomes inaudible. During this time it has traveled over a kilometer! Even this very gradual dissipation of energy occurs mostly as heating of the church's walls and by the leaking of sound to the outside (where it will eventually end up as heat). Under the right conditions (humid air and low frequency), a sound wave in a straight pipe could theoretically travel hundreds of kilometers before being noticeably attenuated.
In general, the absorption of mechanical waves depends a great deal on the chemical composition and microscopic structure of the medium. Ripples on the surface of antifreeze, for instance, die out extremely rapidly compared to ripples on water. For sound waves and surface waves in liquids and gases, what matters is the viscosity of the substance, i.e., whether it flows easily like water or mercury or more sluggishly like molasses or antifreeze. This explains why our intuitive expectation of strong absorption of sound in water is incorrect. Water is a very weak absorber of sound (viz. whale songs and sonar), and our incorrect intuition arises from focusing on the wrong property of the substance: water's high density, which is irrelevant, rather than its low viscosity, which is what matters.
Light is an interesting case, since although it can travel through matter, it is not itself a vibration of any material substance. Thus we can look at the star Sirius, `10^14` km away from us, and be assured that none of its light was absorbed in the vacuum of outer space during its 9-year journey to us. The Hubble Space Telescope routinely observes light that has been on its way to us since the early history of the universe, billions of years ago. Of course the energy of light can be dissipated if it does pass through matter (and the light from distant galaxies is often absorbed if there happen to be clouds of gas or dust in between).
Example 4: Soundproofing
Typical amateur musicians setting out to soundproof their garages tend to think that they should simply cover the walls with the densest possible substance. In fact, sound is not absorbed very strongly even by passing through several inches of wood. A better strategy for soundproofing is to create a sandwich of alternating layers of materials in which the speed of sound is very different, to encourage reflection.
The classic design is alternating layers of fiberglass and plywood. The speed of sound in plywood is very high, due to its stiffness, while its speed in fiberglass is essentially the same as its speed in air. Both materials are fairly good sound absorbers, but sound waves passing through a few inches of them are still not going to be absorbed sufficiently. The point of combining them is that a sound wave that tries to get out will be strongly reflected at each of the fiberglass-plywood boundaries, and will bounce back and forth many times like a ping pong ball. Due to all the back-and-forth motion, the sound may end up traveling a total distance equal to ten times the actual thickness of the soundproofing before it escapes. This is the equivalent of having ten times the thickness of sound-absorbing material.
Example 5: The swim bladder
The swim bladder of a fish, which was first discussed in homework problem 2 in chapter 18, is often located right next to the fish's ear. As discussed in example 1 on page 511, the fish's body is nearly transparent to sound, so it's actually difficult to get any of the sound wave energy to deposit itself in the fish so that the fish can hear it! The physics here is almost exactly the same as the physics of example 4 above, with the gas-filled swim bladder playing the role of the low-density material.
Example 6: Radio transmission
A radio transmitting station, such as a commercial station or an amateur “ham” radio station, must have a length of wire or cable connecting the amplifier to the antenna. The cable and the antenna act as two different media for radio waves, and there will therefore be partial reflection of the waves as they come from the cable to the antenna. If the waves bounce back and forth many times between the amplifier and the antenna, a great deal of their energy will be absorbed. There are two ways to attack the problem. One possibility is to design the antenna so that the speed of the waves in it is as close as possible to the speed of the waves in the cable; this minimizes the amount of reflection. The other method is to connect the amplifier to the antenna using a type of wire or cable that does not strongly absorb the waves. Partial reflection then becomes irrelevant, since all the wave energy will eventually exit through the antenna.
Example 7: The tympanogram
The tympanogram is a medical procedure used to diagnose problems with the middle ear.
The middle ear is a chamber, normally filled with air, lying between the eardrum (tympanic membrane) and the inner ear. It contains a tiny set of bones that act as a system of levers to amplify the motion of the eardrum and transmit it to the inner ear. The air pressure in the inner ear is normally equalized via the Eustachian tube, which connects to the throat; when you feel uncomfortable pressure in your ear while flying, it's because the pressure has not yet equalized. Ear infections or allergies can cause the middle ear to become filled with fluid, and the Eustachian tube can also become blocked, so that the pressure in the inner ear cannot become equalized.
The tympanometer has a probe that is inserted into the ear, with several holes. One hole is used to send a 226 Hz sound wave into the ear canal. The ear has evolved so as to transmit a maximum amount of wave motion to the inner ear. Any change in its physical properties will change its behavior from its normal optimum, so that more sound energy than normal is reflected back. A second hole in the probe senses the reflected wave. If the reflection is stronger than normal, there is probably something wrong with the inner ear.
The full physical analysis is fairly complex. The middle ear has some of the characteristics of a mass oscillating on a spring, but it also has some of the characteristics of a medium that carries waves. Crudely, we could imagine that an infected, fluid-filled middle ear would act as a medium that differed greatly from the air in the outer ear, causing a large amount of reflection.
Equally crudely, we could forget about the wave ideas and think of the middle ear purely as a mass on a spring. We expect resonant behavior, and there is in fact such a resonance, which is typically at a frequency of about 600 Hz in adults, so the 226 Hz frequency emitted by the probe is actually quite far from resonance. If the mechanisms of the middle ear are jammed and cannot vibrate, then it is not possible for energy of the incoming sound wave to be turned into energy of vibration in the middle ear, and therefore by conservation of energy we would expect all of the sound to be reflected.
Sometimes the middle ear's mechanisms can get jammed because of abnormally high or low pressure, because the Eustachian tube is blocked and cannot equalize the pressure with the outside environment. Diagnosing such a condition is the purpose of the third hole in the probe, which is used to vary the pressure in the ear canal. The amount of reflection is measured as a function of this pressure. If the reflection is minimized for some value of the pressure that is different than atmospheric pressure, it indicates that that is the value of the pressure in the middle ear; when the pressures are equalized, the forces on the eardrum cancel out, and it can relax to its normal position, unjamming the middle ear's mechanisms.
Discussion Question
A A sound wave that underwent a pressure-inverting reflection would have its compressions converted to expansions and vice versa. How would its energy and frequency compare with those of the original sound? Would it sound any different? What happens if you swap the two wires where they connect to a stereo speaker, resulting in waves that vibrate in the opposite way?
20.1 Reflection, transmission, and absorption by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.