1.3 Organisms of different sizes with the same shape by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
1.3 Scaling applied to biology (optional)
Organisms of different sizes with the same shape
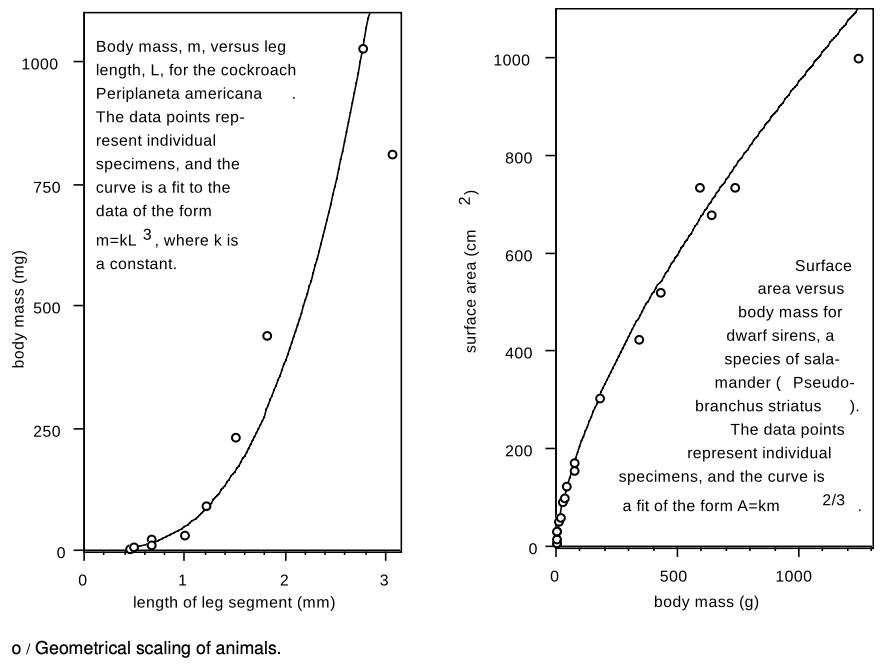
The left-hand panel in figure o shows the approximate validity of the proportionality `mpropL^3` for cockroaches (redrawn from McMahon and Bonner). The scatter of the points around the curve indicates that some cockroaches are proportioned slightly differently from others, but in general the data seem well described by `mpropL^3`. That means that the largest cockroaches the experimenter could raise (is there a 4-H prize?) had roughly the same shape as the smallest ones.
Another relationship that should exist for animals of different sizes shaped in the same way is that between surface area and body mass. If all the animals have the same average density, then body mass should be proportional to the cube of the animal's linear size, `mpropL^3`, while surface area should vary proportionately to `L^2`. Therefore, the animals' surface areas should be proportional to `m^(2"/"3)`. As shown in the right-hand panel of figure o, this relationship appears to hold quite well for the dwarf siren, a type of salamander. Notice how the curve bends over, meaning that the surface area does not increase as quickly as body mass, e.g., a salamander with eight times more body mass will have only four times more surface area.
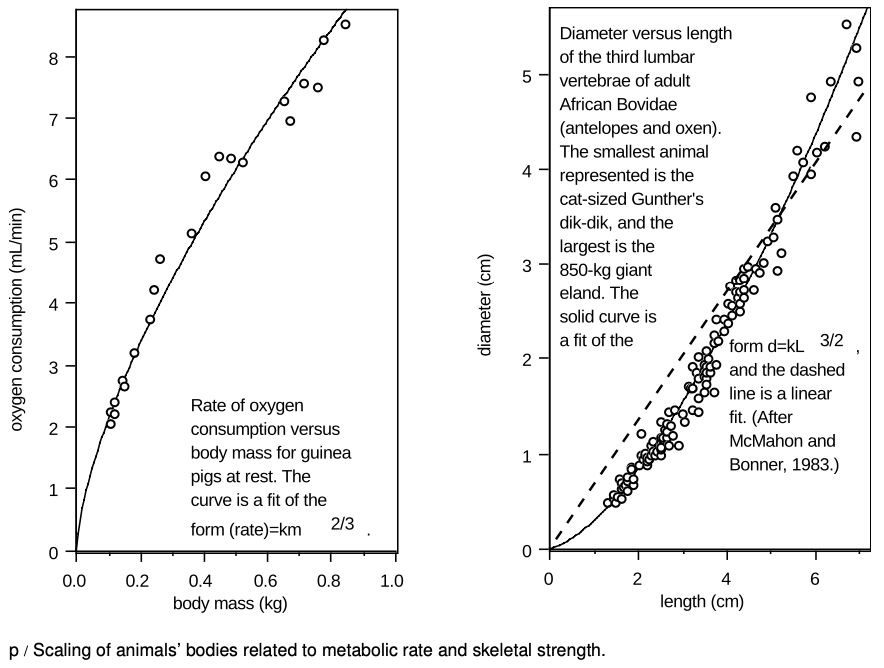
This behavior of the ratio of surface area to mass (or, equivalently, the ratio of surface area to volume) has important consequences for mammals, which must maintain a constant body temperature. It would make sense for the rate of heat loss through the animal's skin to be proportional to its surface area, so we should expect small animals, having large ratios of surface area to volume, to need to produce a great deal of heat in comparison to their size to avoid dying from low body temperature. This expectation is borne out by the data of the left-hand panel of figure p, showing the rate of oxygen consumption of guinea pigs as a function of their body mass. Neither an animal's heat production nor its surface area is convenient to measure, but in order to produce heat, the animal must metabolize oxygen, so oxygen consumption is a good indicator of the rate of heat production. Since surface area is proportional to `m^(2"/"3)`, the proportionality of the rate of oxygen consumption to `m^(2"/"3)` is consistent with the idea that the animal needs to produce heat at a rate in proportion to its surface area. Although the smaller animals metabolize less oxygen and produce less heat in absolute terms, the amount of food and oxygen they must consume is greater in proportion to their own mass. The Etruscan pigmy shrew, weighing in at 2 grams as an adult, is at about the lower size limit for mammals. It must eat continually, consuming many times its body weight each day to survive.
Changes in shape to accommodate changes in size
Large animals also must be able to support their own weight. Returning to the example of the strengths of planks of different sizes, we can see that if the strength of the plank depends on area while its weight depends on volume, then the ratio of strength to weight goes as follows:
`"strength/weight" prop A"/"V prop 1"/"L`.
Thus, the ability of objects to support their own weights decreases inversely in proportion to their linear dimensions. If an object is to be just barely able to support its own weight, then a larger version will have to be proportioned differently, with a different shape.
Since the data on the cockroaches seemed to be consistent with roughly similar shapes within the species, it appears that the ability to support its own weight was not the tightest design constraint that Nature was working under when she designed them. For large animals, structural strength is important. Galileo was the first to quantify this reasoning and to explain why, for instance, a large animal must have bones that are thicker in proportion to their length. Consider a roughly cylindrical bone such as a leg bone or a vertebra. The length of the bone, `L`, is dictated by the overall linear size of the animal, since the animal's skeleton must reach the animal's whole length. We expect the animal's mass to scale as `L^3`, so the strength of the bone must also scale as `L^3`. Strength is proportional to cross-sectional area, as with the wooden planks, so if the diameter of the bone is `d`, then
`dpropL^3`
or
`dpropL^(3"/"2)`.
If the shape stayed the same regardless of size, then all linear dimensions, including `d` and `L`, would be proportional to one another. If our reasoning holds, then the fact that `d` is proportional to `L^(3"/"2)`, not `L`, implies a change in proportions of the bone. As shown in the right-hand panel of figure p, the vertebrae of African Bovidae follow the rule `d∝L^(3"/"2)` fairly well. The vertebrae of the giant eland are as chunky as a coffee mug, while those of a Gunther's dik-dik are as slender as the cap of a pen.
Discussion Questions
A Single-celled animals must passively absorb nutrients and oxygen from their surroundings, unlike humans who have lungs to pump air in and out and a heart to distribute the oxygenated blood throughout their bodies. Even the cells composing the bodies of multicellular animals must absorb oxygen from a nearby capillary through their surfaces. Based on these facts, explain why cells are always microscopic in size.
B The reasoning of the previous question would seem to be contradicted by the fact that human nerve cells in the spinal cord can be as much as a meter long, although their widths are still very small. Why is this possible?
1.3 Organisms of different sizes with the same shape by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.