LM 24.1 The magnetic field Collection
24.1 The magnetic field by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
24.1 The magnetic field
No magnetic monopoles
 If you could play with a handful of electric dipoles and a handful of bar magnets, they would appear very similar. For instance, a pair of bar magnets wants to align themselves head-to-tail, and a pair of electric dipoles does the same thing. (It is unfortunately not that easy to make a permanent electric dipole that can be handled like this, since the charge tends to leak.)
If you could play with a handful of electric dipoles and a handful of bar magnets, they would appear very similar. For instance, a pair of bar magnets wants to align themselves head-to-tail, and a pair of electric dipoles does the same thing. (It is unfortunately not that easy to make a permanent electric dipole that can be handled like this, since the charge tends to leak.)
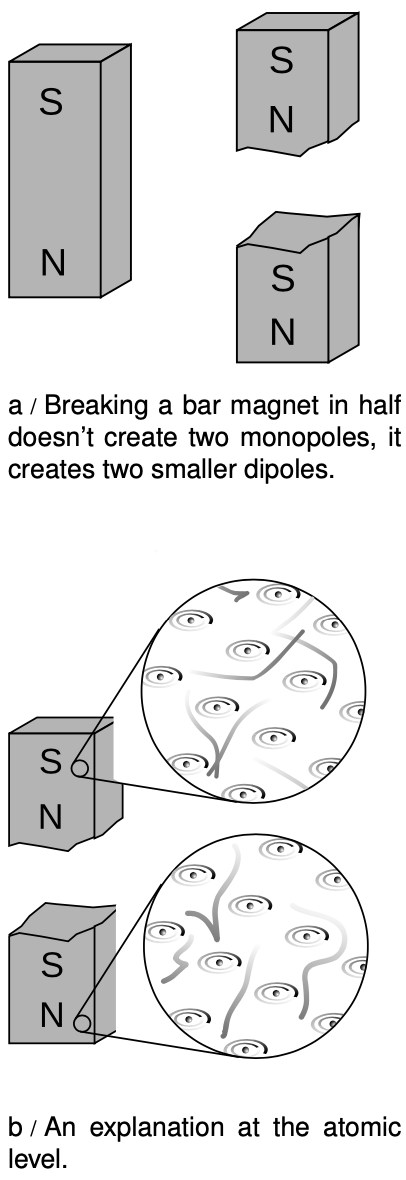
You would eventually notice an important difference between the two types of objects, however. The electric dipoles can be broken apart to form isolated positive charges and negative charges. The two-ended device can be broken into parts that are not two-ended. But if you break a bar magnet in half, a, you will find that you have simply made two smaller two-ended objects.
The reason for this behavior is not hard to divine from our microscopic picture of permanent iron magnets. An electric dipole has extra positive “stuff” concentrated in one end and extra negative in the other. The bar magnet, on the other hand, gets its magnetic properties not from an imbalance of magnetic “stuff” at the two ends but from the orientation of the rotation of its electrons. One end is the one from which we could look down the axis and see the electrons rotating clockwise, and the other is the one from which they would appear to go counterclockwise. There is no difference between the “stuff” in one end of the magnet and the other, b.
Nobody has ever succeeded in isolating a single magnetic pole. In technical language, we say that magnetic monopoles do not seem to exist. Electric monopoles do exist --- that's what charges are.
Electric and magnetic forces seem similar in many ways. Both act at a distance, both can be either attractive or repulsive, and both are intimately related to the property of matter called charge. (Recall that magnetism is an interaction between moving charges.) Physicists's aesthetic senses have been offended for a long time  because this seeming symmetry is broken by the existence of electric monopoles and the absence of magnetic ones. Perhaps some exotic form of matter exists, composed of particles that are magnetic monopoles. If such particles could be found in cosmic rays or moon rocks, it would be evidence that the apparent asymmetry was only an asymmetry in the composition of the universe, not in the laws of physics. For these admittedly subjective reasons, there have been several searches for magnetic monopoles. Experiments have been performed, with negative results, to look for magnetic monopoles embedded in ordinary matter. Soviet physicists in the 1960's made exciting claims that they had created and detected magnetic monopoles in particle accelerators, but there was no success in attempts to reproduce the results there or at other accelerators. The most recent search for magnetic monopoles, done by reanalyzing data from the search for the top quark at Fermilab, turned up no candidates, which shows that either monopoles don't exist in nature or they are extremely massive and thus hard to create in accelerators.
because this seeming symmetry is broken by the existence of electric monopoles and the absence of magnetic ones. Perhaps some exotic form of matter exists, composed of particles that are magnetic monopoles. If such particles could be found in cosmic rays or moon rocks, it would be evidence that the apparent asymmetry was only an asymmetry in the composition of the universe, not in the laws of physics. For these admittedly subjective reasons, there have been several searches for magnetic monopoles. Experiments have been performed, with negative results, to look for magnetic monopoles embedded in ordinary matter. Soviet physicists in the 1960's made exciting claims that they had created and detected magnetic monopoles in particle accelerators, but there was no success in attempts to reproduce the results there or at other accelerators. The most recent search for magnetic monopoles, done by reanalyzing data from the search for the top quark at Fermilab, turned up no candidates, which shows that either monopoles don't exist in nature or they are extremely massive and thus hard to create in accelerators.
Definition of the magnetic field
Since magnetic monopoles don't seem to exist, it would not make much sense to define a magnetic field in terms of the force on a test monopole. Instead, we follow the philosophy of the alternative definition of the electric field, and define the field in terms of the torque on a magnetic test dipole. This is exactly what a magnetic compass does: the needle is a little iron magnet which acts like a magnetic dipole and shows us the direction of the earth's magnetic field.
To define the strength of a magnetic field, however, we need some way of defining the strength of a test dipole, i.e., we need a definition of the magnetic dipole moment. We could use an iron permanent magnet constructed according to certain specifications, but such an object is really an extremely complex system consisting of many iron atoms, only some of which are aligned. A more fundamental standard dipole is a square current loop. This could be little resistive circuit consisting of a square of wire shorting across a battery.
We will find that such a loop, when placed in a magnetic field, experiences a torque that tends to align plane so that its face points in a certain direction. (Since the loop is symmetric, it doesn't care if we rotate it like a wheel without changing the plane in which it lies.) It is this preferred facing direction that we will end up defining as the direction of the magnetic field.
Experiments show if the loop is out of alignment with the field, the torque on it is proportional to the amount of current, and also to the interior area of the loop. The proportionality to current makes sense, since magnetic forces are interactions between moving charges, and current is a measure of the motion of charge. The proportionality to the loop's area is also not hard to understand, because increasing the length of the sides of the square increases both the amount of charge contained in this circular “river” and the amount of leverage supplied for making torque. Two separate physical reasons for a proportionality to length result in an overall proportionality to length squared, which is the same  as the area of the loop. For these reasons, we define the magnetic dipole moment of a square current loop as
as the area of the loop. For these reasons, we define the magnetic dipole moment of a square current loop as
Dm=IA , [definition of the magnetic dipole moment of a square current loop]
We now define the magnetic field in a manner entirely analogous to the second definition of the electric field:
definition of the magnetic field
The magnetic field vector, B, at any location in space is defined by observing the torque exerted on a magnetic test dipole Dmt consisting of a square current loop. The field's magnitude is |B|=τ/Dmtsinθ, where θ is the angle by which the loop is misaligned. The direction of the field is perpendicular to the loop; of the two perpendiculars, we choose the one such that if we look along it, the loop's current is counterclockwise.
We find from this definition that the magnetic field has units of N⋅m/A⋅m2=N/A⋅m. This unwieldy combination of units is abbreviated as the tesla, T=1N/A⋅m. Refrain from memorizing the part about the counterclockwise direction at the end; in section 24.5 we'll see how to understand this in terms of more basic principles.
The nonexistence of magnetic monopoles means that unlike an electric field, d/1, a magnetic one, d/2, can never have sources or sinks. The magnetic field vectors lead in paths that loop back on themselves, without ever converging or diverging at a point.
Relativity
The definition of the tesla as 1N/A?m looks messy, but relativity suggests a simple explanation. We saw in section 23.2 that a particular mixture of electric and magnetic fields appears to be a different mixture in a different frame of reference. In a system of units designed for relativity, E and B have the same units. The SI, which predates relativity, wasn't designed this way, which is also why c is some number with units of m/s rather than simply equaling 1. The SI units of the E and B fields are almost the same: they differ only by a factor of m/s.
Figure e shows that something similar to the parallelogram diagrams developed in ch. 23 also works as a way of representing the transformation of the E and B fields from one frame of reference to another. One frame is moving relative to the other in the x direction, and this mixes certain components of the fields. A dot on the graph represents a particular set of fields, which are seen by each observer according to her own coordinate grid.
24.1 The magnetic field by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Calculators and Collections
Equations
- Comments
- Attachments
- Stats
No comments |
