LM 26.4 The nucleus Collection
26.4 The nucleus by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
26.4 The nucleus
Radioactivity
Becquerel's discovery of radioactivity
 How did physicists figure out that the raisin cookie model was incorrect, and that the atom's positive charge was concentrated in a tiny, central nucleus? The story begins with the discovery of radioactivity by the French chemist Becquerel. Up until radioactivity was discovered, all the processes of nature were thought to be based on chemical reactions, which were rearrangements of combinations of atoms. Atoms exert forces on each other when they are close together, so sticking or unsticking them would either release or store electrical energy. That energy could be converted to and from other forms, as when a plant uses the energy in sunlight to make sugars and carbohydrates, or when a child eats sugar, releasing the energy in the form of kinetic energy.
How did physicists figure out that the raisin cookie model was incorrect, and that the atom's positive charge was concentrated in a tiny, central nucleus? The story begins with the discovery of radioactivity by the French chemist Becquerel. Up until radioactivity was discovered, all the processes of nature were thought to be based on chemical reactions, which were rearrangements of combinations of atoms. Atoms exert forces on each other when they are close together, so sticking or unsticking them would either release or store electrical energy. That energy could be converted to and from other forms, as when a plant uses the energy in sunlight to make sugars and carbohydrates, or when a child eats sugar, releasing the energy in the form of kinetic energy.
Becquerel discovered a process that seemed to release energy from an unknown new source that was not chemical. Becquerel, whose father and grandfather had also been physicists, spent the first twenty years of his professional life as a successful civil engineer, teaching physics on a part-time basis. He was awarded the chair of physics at the Musée d'Histoire Naturelle in Paris after the death of his father, who had previously occupied it. Having now a significant amount of time to devote to physics, he began studying the interaction of light and matter. He became interested in the phenomenon of phosphorescence, in which a substance absorbs energy from light, then releases the energy via a glow that only gradually goes away.
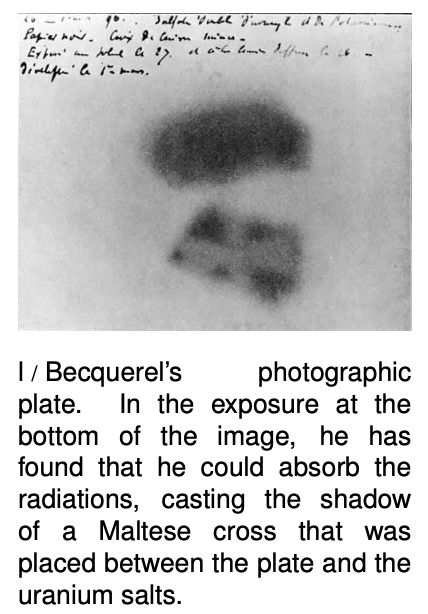 One of the substances he investigated was a uranium compound, the salt UKSO5. One day in 1896, cloudy weather interfered with his plan to expose this substance to sunlight in order to observe its fluorescence. He stuck it in a drawer, coincidentally on top of a blank photographic plate --- the old-fashioned glass-backed counterpart of the modern plastic roll of film. The plate had been carefully wrapped, but several days later when Becquerel checked it in the darkroom before using it, he found that it was ruined, as if it had been completely exposed to light.
One of the substances he investigated was a uranium compound, the salt UKSO5. One day in 1896, cloudy weather interfered with his plan to expose this substance to sunlight in order to observe its fluorescence. He stuck it in a drawer, coincidentally on top of a blank photographic plate --- the old-fashioned glass-backed counterpart of the modern plastic roll of film. The plate had been carefully wrapped, but several days later when Becquerel checked it in the darkroom before using it, he found that it was ruined, as if it had been completely exposed to light.
History provides many examples of scientific discoveries that happened this way: an alert and inquisitive mind decides to investigate a phenomenon that most people would not have worried about explaining. Becquerel first determined by further experiments that the effect was produced by the uranium salt, despite a thick wrapping of paper around the plate that blocked out all light. He tried a variety of compounds, and found that it was the uranium that did it: the effect was produced by any uranium compound, but not by any compound that didn't include uranium atoms. The effect could be at least partially blocked by a sufficient thickness of metal, and he was able to produce silhouettes of coins by interposing them between the uranium and the plate. This indicated that the effect traveled in a straight line., so that it must have been some kind of ray rather than, e.g., the seepage of chemicals through the paper. He used the word “radiations,” since the effect radiated out from the uranium salt.
At this point Becquerel still believed that the uranium atoms were absorbing energy from light and then gradually releasing the energy in the form of the mysterious rays, and this was how he presented it in his first published lecture describing his experiments. Interesting, but not earth-shattering. But he then tried to determine how long it took for the uranium to use up all the energy that had supposedly been stored in it by light, and he found that it never seemed to become inactive, no matter how long he waited. Not only that, but a sample that had been exposed to intense sunlight for a whole afternoon was no more or less effective than a sample that had always been kept inside. Was this a violation of conservation of energy? If the energy didn't come from exposure to light, where did it come from?
Three kinds of “radiations”
Unable to determine the source of the energy directly, turn-of-the-century physicists instead studied the behavior of the “radiations” once they had been emitted. Becquerel had already shown that the radioactivity could penetrate through cloth and paper, so the first obvious thing to do was to investigate in more detail what thickness of material the radioactivity could get through. They soon learned that a certain fraction of the radioactivity's intensity would be eliminated by even a few inches of air, but the remainder was not eliminated by passing through more air. Apparently, then, the radioactivity was a mixture of more than one type, of which one was blocked by air. They then found that of the part that could penetrate air, a further fraction could be eliminated by a piece of paper or a very thin metal foil. What was left after that, however, was a third, extremely penetrating type, some of whose intensity would still remain even after passing through a brick wall. They decided that this showed there were three types of radioactivity, and without having the faintest idea of what they really were, they made up names for them. The least penetrating type was arbitrarily labeled ? (alpha), the first letter of the Greek alphabet, and so on through ? (beta) and finally ? (gamma) for the most penetrating type.
Radium: a more intense source of radioactivity
Tracking down the nature of alphas, betas, and gammas
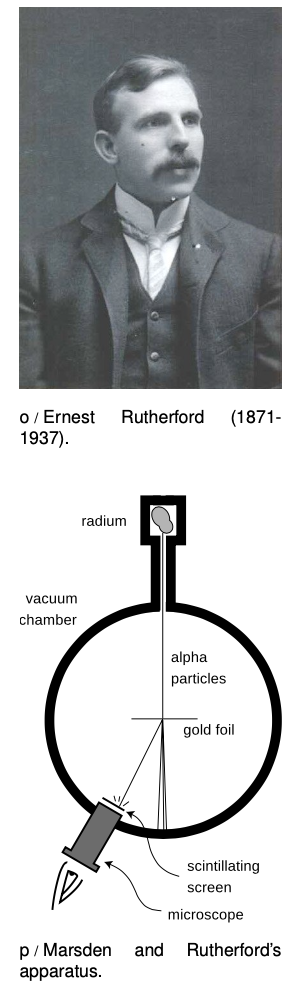
 As radium was becoming available, an apprentice scientist named Ernest Rutherford arrived in England from his native New Zealand and began studying radioactivity at the Cavendish Laboratory. The young colonial's first success was to measure the mass-to-charge ratio of beta rays. The technique was essentially the same as the one Thomson had used to measure the mass-to-charge ratio of cathode rays by measuring their deflections in electric and magnetic fields. The only difference was that instead of the cathode of a vacuum tube, a nugget of radium was used to supply the beta rays. Not only was the technique the same, but so was the result. Beta rays had the same m/q ratio as cathode rays, which suggested they were one and the same. Nowadays, it would make sense simply to use the term “electron,” and avoid the archaic “cathode ray” and “beta particle,” but the old labels are still widely used, and it is unfortunately necessary for physics students to memorize all three names for the same thing.
As radium was becoming available, an apprentice scientist named Ernest Rutherford arrived in England from his native New Zealand and began studying radioactivity at the Cavendish Laboratory. The young colonial's first success was to measure the mass-to-charge ratio of beta rays. The technique was essentially the same as the one Thomson had used to measure the mass-to-charge ratio of cathode rays by measuring their deflections in electric and magnetic fields. The only difference was that instead of the cathode of a vacuum tube, a nugget of radium was used to supply the beta rays. Not only was the technique the same, but so was the result. Beta rays had the same m/q ratio as cathode rays, which suggested they were one and the same. Nowadays, it would make sense simply to use the term “electron,” and avoid the archaic “cathode ray” and “beta particle,” but the old labels are still widely used, and it is unfortunately necessary for physics students to memorize all three names for the same thing.
At first, it seemed that neither alphas or gammas could be deflected in electric or magnetic fields, making it appear that neither was electrically charged. But soon Rutherford obtained a much more powerful magnet, and was able to use it to deflect the alphas but not the gammas. The alphas had a much larger value of m/q than the betas (about 4000 times greater), which was why they had been so hard to deflect. Gammas are uncharged, and were later found to be a form of light.
The m/q ratio of alpha particles turned out to be the same as those of two different types of ions, He++(a helium atom with two missing electrons) and H2+ (two hydrogen atoms bonded into a molecule, with one electron missing), so it seemed likely that they were one or the other of those. The diagram shows a simplified version of Rutherford's ingenious experiment proving that they were He++ ions. The gaseous element radon, an alpha emitter, was introduced into one half of a double glass chamber. The glass wall dividing the chamber was made extremely thin, so that some of the rapidly moving alpha particles were able to penetrate it. The other chamber, which was initially evacuated, gradually began to accumulate a population of alpha particles (which would quickly pick up electrons from their surroundings and become electrically neutral). Rutherford then determined that it was helium gas that had appeared in the second chamber. Thus alpha particles were proved to be He++ ions. The nucleus was yet to be discovered, but in modern terms, we would describe a He++ ion as the nucleus of a He atom.
 To summarize, here are the three types of radiation emitted by radioactive elements, and their descriptions in modern terms:
To summarize, here are the three types of radiation emitted by radioactive elements, and their descriptions in modern terms:

Discussion Question
A Most sources of radioactivity emit alphas, betas, and gammas, not just one of the three. In the radon experiment, how did Rutherford know that he was studying the alphas?
The planetary model
The stage was now set for the unexpected discovery that the positively charged part of the atom was a tiny, dense lump at the atom's center rather than the “cookie dough” of the raisin cookie model. By 1909, Rutherford was an established professor, and had students working under him. For a raw undergraduate named Marsden, he picked a research project he thought would be tedious but straightforward.
It was already known that although alpha particles would be stopped completely by a sheet of paper, they could pass through a sufficiently thin metal foil. Marsden was to work with a gold foil only 1000 atoms thick. (The foil was probably made by evaporating a little gold in a vacuum chamber so that a thin layer would be deposited on a glass microscope slide. The foil would then be lifted off the slide by submerging the slide in water.)
Rutherford had already determined in his previous experiments the speed of the alpha particles emitted by radium, a fantastic 1.5×107m/s. The experimenters in Rutherford's group visualized them as very small, very fast cannonballs penetrating the “cookie dough” part of the big gold atoms. A piece of paper has a thickness of a hundred thousand atoms or so, which would be sufficient to stop them completely, but crashing through a thousand would only slow them a little and turn them slightly off of their original paths.
Marsden's supposedly ho-hum assignment was to use the apparatus shown in figure p to measure how often alpha particles were deflected at various angles. A tiny lump of radium in a box emitted alpha particles, and a thin beam was created by blocking all the alphas except those that happened to pass out through a tube. Typically deflected in the gold by only a small amount, they would reach a screen very much like the screen of a TV's picture tube, which would make a flash of light when it was hit. Here is the first example we have encountered of an experiment in which a beam of particles is detected one at a time. This was possible because each alpha particle carried so much kinetic energy; they were moving at about the same speed as the electrons in the Thomson experiment, but had ten thousand times more mass.
Marsden sat in a dark room, watching the apparatus hour after hour and recording the number of flashes with the screen moved to various angles. The rate of the flashes was highest when he set the screen at an angle close to the line of the alphas' original path, but if he watched an area farther off to the side, he would also occasionally see an alpha that had been deflected through a larger angle. After seeing a few of these, he got the crazy idea of moving the screen to see if even larger angles ever occurred, perhaps even angles larger than 90 degrees.
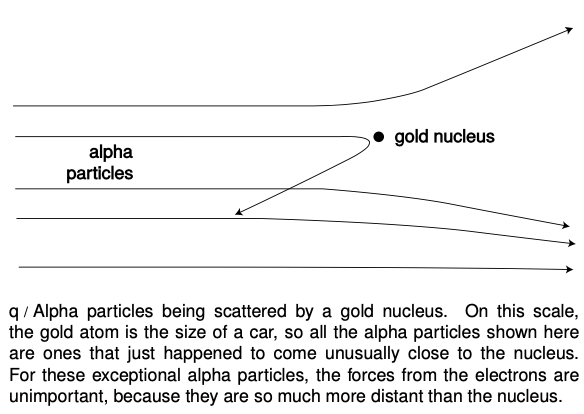
 The crazy idea worked: a few alpha particles were deflected through angles of up to 180 degrees, and the routine experiment had become an epoch-making one. Rutherford said, “We have been able to get some of the alpha particles coming backwards. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.” Explanations were hard to come by in the raisin cookie model. What intense electrical forces could have caused some of the alpha particles, moving at such astronomical speeds, to change direction so drastically? Since each gold atom was electrically neutral, it would not exert much force on an alpha particle outside it. True, if the alpha particle was very near to or inside of a particular atom, then the forces would not necessarily cancel out perfectly; if the alpha particle happened to come very close to a particular electron, the 1r2 form of the Coulomb force law would make for a very strong force. But Marsden and Rutherford knew that an alpha particle was 8000 times more massive than an electron, and it is simply not possible for a more massive object to rebound backwards from a collision with a less massive object while conserving momentum and energy. It might be possible in principle for a particular alpha to follow a path that took it very close to one electron, and then very close to another electron, and so on, with the net result of a large deflection, but careful calculations showed that such multiple “close encounters” with electrons would be millions of times too rare to explain what was actually observed.
The crazy idea worked: a few alpha particles were deflected through angles of up to 180 degrees, and the routine experiment had become an epoch-making one. Rutherford said, “We have been able to get some of the alpha particles coming backwards. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.” Explanations were hard to come by in the raisin cookie model. What intense electrical forces could have caused some of the alpha particles, moving at such astronomical speeds, to change direction so drastically? Since each gold atom was electrically neutral, it would not exert much force on an alpha particle outside it. True, if the alpha particle was very near to or inside of a particular atom, then the forces would not necessarily cancel out perfectly; if the alpha particle happened to come very close to a particular electron, the 1r2 form of the Coulomb force law would make for a very strong force. But Marsden and Rutherford knew that an alpha particle was 8000 times more massive than an electron, and it is simply not possible for a more massive object to rebound backwards from a collision with a less massive object while conserving momentum and energy. It might be possible in principle for a particular alpha to follow a path that took it very close to one electron, and then very close to another electron, and so on, with the net result of a large deflection, but careful calculations showed that such multiple “close encounters” with electrons would be millions of times too rare to explain what was actually observed.
At this point, Rutherford and Marsden dusted off an unpopular and neglected model of the atom, in which all the electrons orbited around a small, positively charged core or “nucleus,” just like the planets orbiting around the sun. All the positive charge and nearly all the mass of the atom would be concentrated in the nucleus, rather than spread throughout the atom as in the raisin cookie model. The positively charged alpha particles would be repelled by the gold atom's nucleus, but most of the alphas would not come close enough to any nucleus to have their paths drastically altered. The few that did come close to a nucleus, however, could rebound backwards from a single such encounter, since the nucleus of a heavy gold atom would be fifty times more massive than an alpha particle. It turned out that it was not even too difficult to derive a formula giving the relative frequency of deflections through various angles, and this calculation agreed with the data well enough (to within 15%), considering the difficulty in getting good experimental statistics on the rare, very large angles.
What had started out as a tedious exercise to get a student started in science had ended as a revolution in our understanding of nature. Indeed, the whole thing may sound a little too much like a moralistic fable of the scientific method with overtones of the Horatio Alger genre. The skeptical reader may wonder why the planetary model was ignored so thoroughly until Marsden and Rutherford's discovery. Is science really more of a sociological enterprise, in which certain ideas become accepted by the establishment, and other, equally plausible explanations are arbitrarily discarded? Some social scientists are currently ruffling a lot of scientists' feathers with critiques very much like this, but in this particular case, there were very sound reasons for rejecting the planetary model. As you'll learn in more detail later in this course, any charged particle that undergoes an acceleration dissipate energy in the form of light. In the planetary model, the electrons were orbiting the nucleus in circles or ellipses, which meant they were undergoing acceleration, just like the acceleration you feel in a car going around a curve. They should have dissipated energy as light, and eventually they should have lost all their energy. Atoms don't spontaneously collapse like that, which was why the raisin cookie model, with its stationary electrons, was originally preferred. There were other problems as well. In the planetary model, the one-electron atom would have to be flat, which would be inconsistent with the success of molecular modeling with spherical balls representing hydrogen and atoms. These molecular models also seemed to work best if specific sizes were used for different atoms, but there is no obvious reason in the planetary model why the radius of an electron's orbit should be a fixed number. In view of the conclusive Marsden-Rutherford results, however, these became fresh puzzles in atomic physics, not reasons for disbelieving the planetary model.
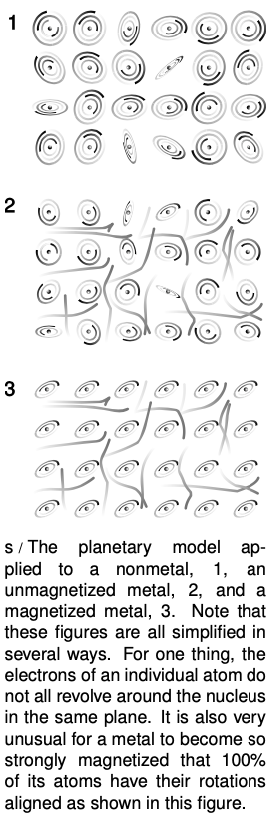 Some phenomena explained with the planetary model
Some phenomena explained with the planetary model
The planetary model may not be the ultimate, perfect model of the atom, but don't underestimate its power. It already allows us to visualize correctly a great many phenomena.
As an example, let's consider the distinctions among nonmetals, metals that are magnetic, and metals that are nonmagnetic. As shown in figure s, a metal differs from a nonmetal because its outermost electrons are free to wander rather than owing their allegiance to a particular atom. A metal that can be magnetized is one that is willing to line up the rotations of some of its electrons so that their axes are parallel. Recall that magnetic forces are forces made by moving charges; we have not yet discussed the mathematics and geometry of magnetic forces, but it is easy to see how random orientations of the atoms in the nonmagnetic substance would lead to cancellation of the forces.
Even if the planetary model does not immediately answer such questions as why one element would be a metal and another a nonmetal, these ideas would be difficult or impossible to conceptualize in the raisin cookie model.
Discussion Question
A In reality, charges of the same type repel one another and charges of different types are attracted. Suppose the rules were the other way around, giving repulsion between opposite charges and attraction between similar ones. What would the universe be like?
Atomic number
As alluded to in a discussion question in the previous section, scientists of this period had only a very approximate idea of how many units of charge resided in the nuclei of the various chemical elements. Although we now associate the number of units of nuclear charge with the element's position on the periodic table, and call it the atomic number, they had no idea that such a relationship existed. Mendeleev's table just seemed like an organizational tool, not something with any necessary physical significance. And everything Mendeleev had done seemed equally valid if you turned the table upside-down or reversed its left and right sides, so even if you wanted to number the elements sequentially with integers, there was an ambiguity as to how to do it. Mendeleev's original table was in fact upside-down compared to the modern one.
In the period immediately following the discovery of the nucleus, physicists only had rough estimates of the charges of the various nuclei. In the case of the very lightest nuclei, they simply found the maximum number of electrons they could strip off by various methods: chemical reactions, electric sparks, ultraviolet light, and so on. For example they could easily strip off one or two electrons from helium, making He+ or He++, but nobody could make He+++, presumably because the nuclear charge of helium was only +2e. Unfortunately only a few of the lightest elements could be stripped completely, because the more electrons were stripped off, the greater the positive net charge remaining, and the more strongly the rest of the negatively charged electrons would be held on. The heavy elements' atomic numbers could only be roughly extrapolated from the light elements, where the atomic number was about half the atom's mass expressed in units of the mass of a hydrogen atom. Gold, for example, had a mass about 197 times that of hydrogen, so its atomic number was estimated to be about half that, or somewhere around 100. We now know it to be 79.
How did we finally find out? The riddle of the nuclear charges was at last successfully attacked using two different techniques, which gave consistent results. One set of experiments, involving x-rays, was performed by the young Henry Mosely, whose scientific brilliance was soon to be sacrificed in a battle between European imperialists over who would own the Dardanelles, during that pointless conflict then known as the War to End All Wars, and now referred to as World War I.
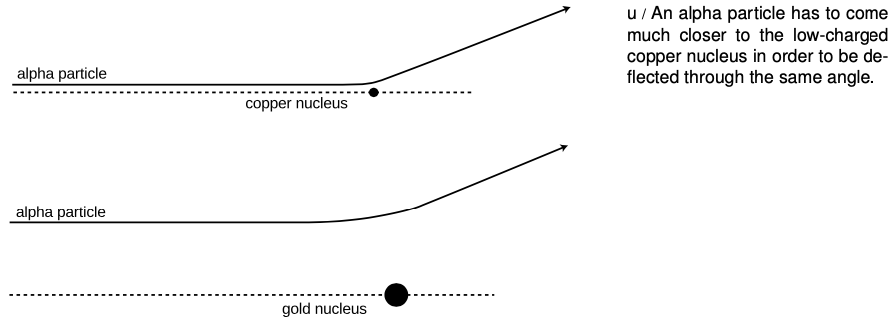
Since Mosely's analysis requires several concepts with which you are not yet familiar, we will instead describe the technique used by James Chadwick at around the same time. An added bonus of describing Chadwick's experiments is that they presaged the important modern technique of studying collisions of subatomic particles. In grad school, I worked with a professor whose thesis adviser's thesis adviser was Chadwick, and he related some interesting stories about the man. Chadwick was apparently a little nutty and a complete fanatic about science, to the extent that when he was held in a German prison camp during World War II, he managed to cajole his captors into allowing him to scrounge up parts from broken radios so that he could attempt to do physics experiments.
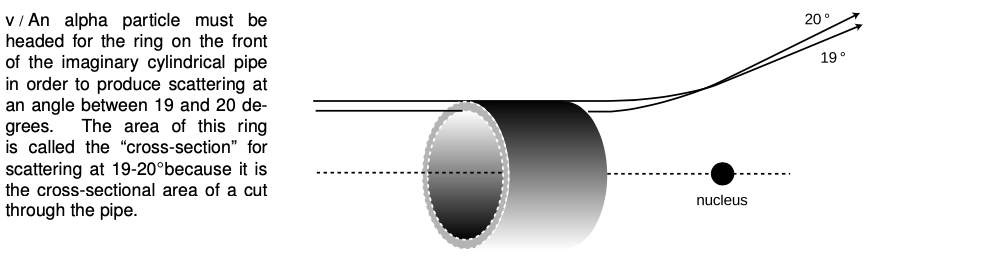
Chadwick's experiment worked like this. Suppose you perform two Rutherford-type alpha scattering measurements, first one with a gold foil as a target as in Rutherford's original experiment, and then one with a copper foil. It is possible to get large angles of deflection in both cases, but as shown in figure v, the alpha particle must be heading almost straight for the copper nucleus to get the same angle of deflection that would have occurred with an alpha that was much farther off the mark; the gold nucleus' charge is so much greater than the copper's that it exerts a strong force on the alpha particle even from far off. The situation is very much like that of a blindfolded person playing darts. Just as it is impossible to aim an alpha particle at an individual nucleus in the target, the blindfolded person cannot really aim the darts. Achieving a very close encounter with the copper atom would be akin to hitting an inner circle on the dartboard. It's much more likely that one would have the luck to hit the outer circle, which covers a greater number of square inches. By analogy, if you measure the frequency with which alphas are scattered by copper at some particular angle, say between 19 and 20 degrees, and then perform the same measurement at the same angle with gold, you get a much higher percentage for gold than for copper.
In fact, the numerical ratio of the two nuclei's charges can be derived from this same experimentally determined ratio. Using the standard notation Z for the atomic number (charge of the nucleus divided by e), the following equation can be proved (example 4):
Z2goldZ2copper=number of alphas scattered by gold at 19-20°number of alphas scattered by copper at 19-20°
By making such measurements for targets constructed from all the elements, one can infer the ratios of all the atomic numbers, and since the atomic numbers of the light elements were already known, atomic numbers could be assigned to the entire periodic table. According to Mosely, the atomic numbers of copper, silver and platinum were 29, 47, and 78, which corresponded well with their positions on the periodic table. Chadwick's figures for the same elements were 29.3, 46.3, and 77.4, with error bars of about 1.5 times the fundamental charge, so the two experiments were in good agreement.
The point here is absolutely not that you should be ready to plug numbers into the above equation for a homework or exam question! My overall goal in this chapter is to explain how we know what we know about atoms. An added bonus of describing Chadwick's experiment is that the approach is very similar to that used in modern particle physics experiments, and the ideas used in the analysis are closely related to the now-ubiquitous concept of a “cross-section.” In the dartboard analogy, the cross-section would be the area of the circular ring you have to hit. The reasoning behind the invention of the term “cross-section” can be visualized as shown in figure v. In this language, Rutherford's invention of the planetary model came from his unexpected discovery that there was a nonzero cross-section for alpha scattering from gold at large angles, and Chadwick confirmed Mosely's determinations of the atomic numbers by measuring cross-sections for alpha scattering.
Example 4: Proof of the relationship between Z and scattering
The equation above can be derived by the following not very rigorous proof. To deflect the alpha particle by a certain angle requires that it acquire a certain momentum component in the direction perpendicular to its original momentum. Although the nucleus's force on the alpha particle is not constant, we can pretend that it is approximately constant during the time when the alpha is within a distance equal to, say, 150% of its distance of closest approach, and that the force is zero before and after that part of the motion. (If we chose 120% or 200%, it shouldn't make any difference in the final result, because the final result is a ratio, and the effects on the numerator and denominator should cancel each other.) In the approximation of constant force, the change in the alpha's perpendicular momentum component is then equal to FΔt. The Coulomb force law says the force is proportional to Z/r2. Although r does change somewhat during the time interval of interest, it's good enough to treat it as a constant number, since we're only computing the ratio between the two experiments' results. Since we are approximating the force as acting over the time during which the distance is not too much greater than the distance of closest approach, the time interval Δt must be proportional to r, and the sideways momentum imparted to the alpha, FΔt, is proportional to (Z/r2)r, or Z/r. If we're comparing alphas scattered at the same angle from gold and from copper, then Δp is the same in both cases, and the proportionality Δp?Z/r tells us that the ones scattered from copper at that angle had to be headed in along a line closer to the central axis by a factor equaling Zgold/Zcopper. If you imagine a “dartboard ring” that the alphas have to hit, then the ring for the gold experiment has the same proportions as the one for copper, but it is enlarged by a factor equal to Zgold/Zcopper. That is, not only is the radius of the ring greater by that factor, but unlike the rings on a normal dartboard, the thickness of the outer ring is also greater in proportion to its radius. When you take a geometric shape and scale it up in size like a photographic enlargement, its area is increased in proportion to the square of the enlargement factor, so the area of the dartboard ring in the gold experiment is greater by a factor equal to (Zgold/Zcopper)2. Since the alphas are aimed entirely randomly, the chances of an alpha hitting the ring are in proportion to the area of the ring, which proves the equation given above.
As an example of the modern use of scattering experiments and cross-section measurements, you may have heard of the recent experimental evidence for the existence of a particle called the top quark. Of the twelve subatomic particles currently believed to be the smallest constituents of matter, six form a family called the quarks, distinguished from the other six by the intense attractive forces that make the quarks stick to each other. (The other six consist of the electron plus five other, more exotic particles.) The only two types of quarks found in naturally occurring matter are the “up quark” and “down quark,” which are what protons and neutrons are made of, but four other types were theoretically predicted to exist, for a total of six. (The whimsical term “quark” comes from a line by James Joyce reading “Three quarks for master Mark.”) Until recently, only five types of quarks had been proven to exist via experiments, and the sixth, the top quark, was only theorized. There was no hope of ever detecting a top quark directly, since it is radioactive, and only exists for a zillionth of a second before evaporating. Instead, the researchers searching for it at the Fermi National Accelerator Laboratory near Chicago measured cross-sections for scattering of nuclei off of other nuclei. The experiment was much like those of Rutherford and Chadwick, except that the incoming nuclei had to be boosted to much higher speeds in a particle accelerator. The resulting encounter with a target nucleus was so violent that both nuclei were completely demolished, but, as Einstein proved, energy can be converted into matter, and the energy of the collision creates a spray of exotic, radioactive particles, like the deadly shower of wood fragments produced by a cannon ball in an old naval battle. Among those particles were some top quarks. The cross-sections being measured were the cross-sections for the production of certain combinations of these secondary particles. However different the details, the principle was the same as that employed at the turn of the century: you smash things together and look at the fragments that fly off to see what was inside them. The approach has been compared to shooting a clock with a rifle and then studying the pieces that fly off to figure out how the clock worked.
Discussion Questions
A The diagram, showing alpha particles being deflected by a gold nucleus, was drawn with the assumption that alpha particles came in on lines at many different distances from the nucleus. Why wouldn't they all come in along the same line, since they all came out through the same tube?
B Why does it make sense that, as shown in the figure, the trajectories that result in 19° and 20° scattering cross each other?
C Rutherford knew the velocity of the alpha particles emitted by radium, and guessed that the positively charged part of a gold atom had a charge of about +100e (we now know it is +79e). Considering the fact that some alpha particles were deflected by 180°, how could he then use conservation of energy to derive an upper limit on the size of a gold nucleus? (For simplicity, assume the size of the alpha particle is negligible compared to that of the gold nucleus, and ignore the fact that the gold nucleus recoils a little from the collision, picking up a little kinetic energy.)
The structure of nuclei
The proton
The fact that the nuclear charges were all integer multiples of e suggested to many physicists that rather than being a point like object, the nucleus might contain smaller particles having individual charges of +e. Evidence in favor of this idea was not long in arriving. Rutherford reasoned that if he bombarded the atoms of a very light element with alpha particles, the small charge of the target nuclei would give a very weak repulsion. Perhaps those few alpha particles that happened to arrive on head-on collision courses would get so close that they would physically crash into some of the target nuclei. An alpha particle is itself a nucleus, so this would be a collision between two nuclei, and a violent one due to the high speeds involved. Rutherford hit pay dirt in an experiment with alpha particles striking a target containing nitrogen atoms. Charged particles were detected flying out of the target like parts flying off of cars in a high-speed crash. Measurements of the deflection of these particles in electric and magnetic fields showed that they had the same charge-to-mass ratio as singly-ionized hydrogen atoms. Rutherford concluded that these were the conjectured singly-charged particles that held the charge of the nucleus, and they were later named protons. The hydrogen nucleus consists of a single proton, and in general, an element's atomic number gives the number of protons contained in each of its nuclei. The mass of the proton is about 1800 times greater than the mass of the electron.
The neutron
It would have been nice and simple if all the nuclei could have been built only from protons, but that couldn't be the case. If you spend a little time looking at a periodic table, you will soon notice that although some of the atomic masses are very nearly integer multiples of hydrogen's mass, many others are not. Even where the masses are close whole numbers, the masses of an element other than hydrogen is always greater than its atomic number, not equal to it. Helium, for instance, has two protons, but its mass is four times greater than that of hydrogen.
Chadwick cleared up the confusion by proving the existence of a new subatomic particle. Unlike the electron and proton, which are electrically charged, this particle is electrically neutral, and he named it the neutron. Chadwick's experiment has been described in detail in section 14.2, but briefly the method was to expose a sample of the light element beryllium to a stream of alpha particles from a lump of radium. Beryllium has only four protons, so an alpha that happens to be aimed directly at a beryllium nucleus can actually hit it rather than being stopped short of a collision by electrical repulsion. Neutrons were observed as a new form of radiation emerging from the collisions, and Chadwick correctly inferred that they were previously unsuspected components of the nucleus that had been knocked out. As described earlier, Chadwick also determined the mass of the neutron; it is very nearly the same as that of the proton.
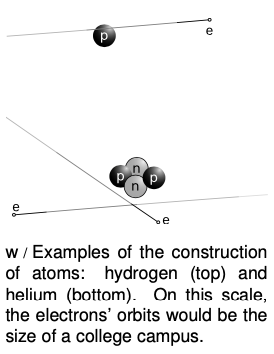 To summarize, atoms are made of three types of particles:
To summarize, atoms are made of three types of particles:
| charge | mass in units of the proton’s mass | location in atom | |
| proton | + e | 1 | in nucleus |
| neutron | 0 | 1.001 | in nucleus |
| electron | - e | 1/1836 | orbiting nucleus |
The existence of neutrons explained the mysterious masses of the elements. Helium, for instance, has a mass very close to four times greater than that of hydrogen. This is because it contains two neutrons in addition to its two protons. The mass of an atom is essentially determined by the total number of neutrons and protons. The total number of neutrons plus protons is therefore referred to as the atom's mass number.
Isotopes
We now have a clear interpretation of the fact that helium is close to four times more massive than hydrogen, and similarly for all the atomic masses that are close to an integer multiple of the mass of hydrogen. But what about copper, for instance, which had an atomic mass 63.5 times that of hydrogen? It didn't seem reasonable to think that it possessed an extra half of a neutron! The solution was found by measuring the mass-to-charge ratios of singly-ionized atoms (atoms with one electron removed). The technique is essentially that same as the one used by Thomson for cathode rays, except that whole atoms do not spontaneously leap out of the surface of an object as electrons sometimes do. Figure x shows an example of how the ions can be created and injected between the charged plates for acceleration.
Injecting a stream of copper ions into the device, we find a surprise --- the beam splits into two parts! Chemists had elevated to dogma the assumption that all the atoms of a given element were identical, but we find that 69% of copper atoms have one mass, and 31% have another. Not only that, but both masses are very nearly integer multiples of the mass of hydrogen (63 and 65, respectively). Copper gets its chemical identity from the number of protons in its nucleus, 29, since chemical reactions work by electric forces. But apparently some copper atoms have 63?29=34 neutrons while others have 65?29=36. The atomic mass of copper, 63.5, reflects the proportions of the mixture of the mass-63 and mass-65 varieties. The different mass varieties of a given element are called isotopes of that element.
 Isotopes can be named by giving the mass number as a subscript to the left of the chemical symbol, e.g., 65Cu. Examples:
Isotopes can be named by giving the mass number as a subscript to the left of the chemical symbol, e.g., 65Cu. Examples:
| protons | neutrons | mass number | |
| 1H | 1 | 0 | 0+1 = 1 |
| 4He | 2 | 2 | 2+2 = 4 |
| 12C | 6 | 6 | 6+6 = 12 |
| 14C | 6 | 8 | 6+8 = 14 |
| 262Ha | 105 | 157 | 105+157 = 262 |
self-check:
Why are the positive and negative charges of the accelerating plates reversed in the isotope-separating apparatus compared to the Thomson apparatus?
(answer in the back of the PDF version of the book)
Chemical reactions are all about the exchange and sharing of electrons: the nuclei have to sit out this dance because the forces of electrical repulsion prevent them from ever getting close enough to make contact with each other. Although the protons do have a vitally important effect on chemical processes because of their electrical forces, the neutrons can have no effect on the atom's chemical reactions. It is not possible, for instance, to separate 63Cu from 65Cu by chemical reactions. This is why chemists had never realized that different isotopes existed. (To be perfectly accurate, different isotopes do behave slightly differently because the more massive atoms move more sluggishly and therefore react with a tiny bit less intensity. This tiny difference is used, for instance, to separate out the isotopes of uranium needed to build a nuclear bomb. The smallness of this effect makes the separation process a slow and difficult one, which is what we have to thank for the fact that nuclear weapons have not been built by every terrorist cabal on the planet.)
Sizes and shapes of nuclei
Matter is nearly all nuclei if you count by weight, but in terms of volume nuclei don't amount to much. The radius of an individual neutron or proton is very close to 1 fm (1 fm=10^(?15) m), so even a big lead nucleus with a mass number of 208 still has a diameter of only about 13 fm, which is ten thousand times smaller than the diameter of a typical atom. Contrary to the usual imagery of the nucleus as a small sphere, it turns out that many nuclei are somewhat elongated, like an American football, and a few have exotic asymmetric shapes like pears or kiwi fruits.
Discussion Questions
A Suppose the entire universe was in a (very large) cereal box, and the nutritional labeling was supposed to tell a godlike consumer what percentage of the contents was nuclei. Roughly what would the percentage be like if the labeling was according to mass? What if it was by volume?

The strong nuclear force, alpha decay and fission
 Once physicists realized that nuclei consisted of positively charged protons and uncharged neutrons, they had a problem on their hands. The electrical forces among the protons are all repulsive, so the nucleus should simply fly apart! The reason all the nuclei in your body are not spontaneously exploding at this moment is that there is another force acting. This force, called the strong nuclear force, is always attractive, and acts between neutrons and neutrons, neutrons and protons, and protons and protons with roughly equal strength. The strong nuclear force does not have any effect on electrons, which is why it does not influence chemical reactions.
Once physicists realized that nuclei consisted of positively charged protons and uncharged neutrons, they had a problem on their hands. The electrical forces among the protons are all repulsive, so the nucleus should simply fly apart! The reason all the nuclei in your body are not spontaneously exploding at this moment is that there is another force acting. This force, called the strong nuclear force, is always attractive, and acts between neutrons and neutrons, neutrons and protons, and protons and protons with roughly equal strength. The strong nuclear force does not have any effect on electrons, which is why it does not influence chemical reactions.
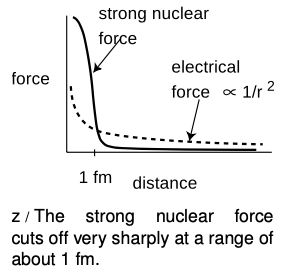
Unlike electric forces, whose strengths are given by the simple Coulomb force law, there is no simple formula for how the strong nuclear force depends on distance. Roughly speaking, it is effective over ranges of ~1 fm, but falls off extremely quickly at larger distances (much faster than 1"/"r^2). Since the radius of a neutron or proton is about 1 fm, that means that when a bunch of neutrons and protons are packed together to form a nucleus, the strong nuclear force is effective only between neighbors.
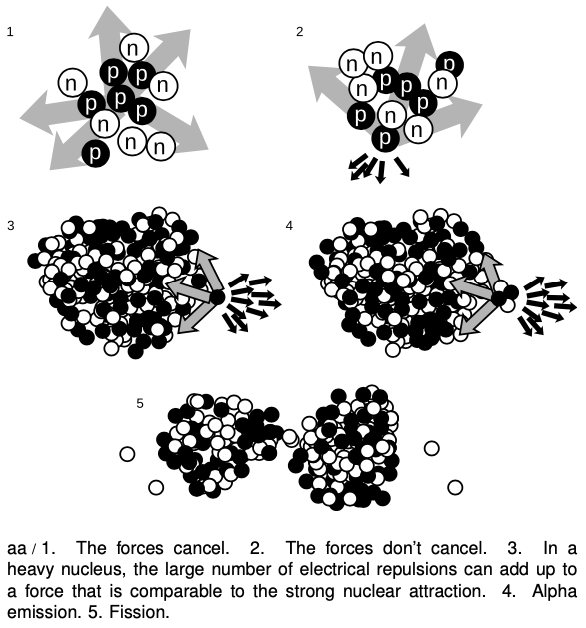 Figure aa illustrates how the strong nuclear force acts to keep ordinary nuclei together, but is not able to keep very heavy nuclei from breaking apart. In aa/1, a proton in the middle of a carbon nucleus feels an attractive strong nuclear force (arrows) from each of its nearest neighbors. The forces are all in different directions, and tend to cancel out. The same is true for the repulsive electrical forces (not shown). In figure aa/2, a proton at the edge of the nucleus has neighbors only on one side, and therefore all the strong nuclear forces acting on it are tending to pull it back in. Although all the electrical forces from the other five protons (dark arrows) are all pushing it out of the nucleus, they are not sufficient to overcome the strong nuclear forces.
Figure aa illustrates how the strong nuclear force acts to keep ordinary nuclei together, but is not able to keep very heavy nuclei from breaking apart. In aa/1, a proton in the middle of a carbon nucleus feels an attractive strong nuclear force (arrows) from each of its nearest neighbors. The forces are all in different directions, and tend to cancel out. The same is true for the repulsive electrical forces (not shown). In figure aa/2, a proton at the edge of the nucleus has neighbors only on one side, and therefore all the strong nuclear forces acting on it are tending to pull it back in. Although all the electrical forces from the other five protons (dark arrows) are all pushing it out of the nucleus, they are not sufficient to overcome the strong nuclear forces.
In a very heavy nucleus, aa/3, a proton that finds itself near the edge has only a few neighbors close enough to attract it significantly via the strong nuclear force, but every other proton in the nucleus exerts a repulsive electrical force on it. If the nucleus is large enough, the total electrical repulsion may be sufficient to overcome the attraction of the strong force, and the nucleus may spit out a proton. Proton emission is fairly rare, however; a more common type of radioactive decay1 in heavy nuclei is alpha decay, shown in aa/4. The imbalance of the forces is similar, but the chunk that is ejected is an alpha particle (two protons and two neutrons) rather than a single proton.
It is also possible for the nucleus to split into two pieces of roughly equal size, aa/5, a process known as fission. Note that in addition to the two large fragments, there is a spray of individual neutrons. In a nuclear fission bomb or a nuclear fission reactor, some of these neutrons fly off and hit other nuclei, causing them to undergo fission as well. The result is a chain reaction.
When a nucleus is able to undergo one of these processes, it is said to be radioactive, and to undergo radioactive decay. Some of the naturally occurring nuclei on earth are radioactive. The term “radioactive” comes from Becquerel's image of rays radiating out from something, not from radio waves, which are a whole different phenomenon. The term “decay” can also be a little misleading, since it implies that the nucleus turns to dust or simply disappears -- actually it is splitting into two new nuclei with an the same total number of neutrons and protons, so the term “radioactive transformation” would have been more appropriate. Although the original atom's electrons are mere spectators in the process of weak radioactive decay, we often speak loosely of “radioactive atoms” rather than “radioactive nuclei.”
Randomness in physics
How does an atom decide when to decay? We might imagine that it is like a termite-infested house that gets weaker and weaker, until finally it reaches the day on which it is destined to fall apart. Experiments, however, have not succeeded in detecting such “ticking clock” hidden below the surface; the evidence is that all atoms of a given isotope are absolutely identical. Why, then, would one uranium atom decay today while another lives for another million years? The answer appears to be that it is entirely random. We can make general statements about the average time required for a certain isotope to decay, or how long it will take for half the atoms in a sample to decay (its half-life), but we can never predict the behavior of a particular atom.
This is the first example we have encountered of an inescapable randomness in the laws of physics. If this kind of randomness makes you uneasy, you're in good company. Einstein's famous quote is “...I am convinced that He [God] does not play dice.“ Einstein's distaste for randomness, and his association of determinism with divinity, goes back to the Enlightenment conception of the universe as a gigantic piece of clockwork that only had to be set in motion initially by the Builder. Physics had to be entirely rebuilt in the 20th century to incorporate the fundamental randomness of physics, and this modern revolution is the topic of chapters 33-26. In particular, we will delay the mathematical development of the half-life concept until then.
The weak nuclear force; beta decay
All the nuclear processes we've discussed so far have involved rearrangements of neutrons and protons, with no change in the total number of neutrons or the total number of protons. Now consider the proportions of neutrons and protons in your body and in the planet earth: neutrons and protons are roughly equally numerous in your body's carbon and oxygen nuclei, and also in the nickel and iron that make up most of the earth. The proportions are about 50-50. But, as discussed in more detail on p. 771, the only chemical elements produced in any significant quantities by the big bang2 were hydrogen (about 90%) and helium (about 10%). If the early universe was almost nothing but hydrogen atoms, whose nuclei are protons, where did all those neutrons come from?
The answer is that there is another nuclear force, the weak nuclear force, that is capable of transforming neutrons into protons and vice-versa. Two possible reactions are
n->p+e^-+barnu [electron decay]
and
p->n+e^++nu. [positron decay]
(There is also a third type called electron capture, in which a proton grabs one of the atom's electrons and they produce a neutron and a neutrino.)
Whereas alpha decay and fission are just a redivision of the previously existing particles, these reactions involve the destruction of one particle and the creation of three new particles that did not exist before.
There are three new particles here that you have never previously encountered. The symbol e^+ stands for an antielectron, which is a particle just like the electron in every way, except that its electric charge is positive rather than negative. Antielectrons are also known as positrons. Nobody knows why electrons are so common in the universe and antielectrons are scarce. When an antielectron encounters an electron, they annihilate each other, producing gamma rays, and this is the fate of all the antielectrons that are produced by natural radioactivity on earth. Antielectrons are an example of antimatter. A complete atom of antimatter would consist of antiprotons, antielectrons, and antineutrons. Although individual particles of antimatter occur commonly in nature due to natural radioactivity and cosmic rays, only a few complete atoms of antihydrogen have ever been produced artificially.
The notation nu stands for a particle called a neutrino, and barnu means an antineutrino. Neutrinos and antineutrinos have no electric charge (hence the name).
We can now list all four of the known fundamental forces of physics:
- gravity
- electromagnetism
- strong nuclear force
- weak nuclear force
The other forces we have learned about, such as friction and the normal force, all arise from electromagnetic interactions between atoms, and therefore are not considered to be fundamental forces of physics.
Example 5: Decay of 212Pb
As an example, consider the radioactive isotope of lead 212Pb. It contains 82 protons and 130 neutrons. It decays by the process n->p + e^(-)+barnu. The newly created proton is held inside the nucleus by the strong nuclear force, so the new nucleus contains 83 protons and 129 neutrons. Having 83 protons makes it the element bismuth, so it will be an atom of 212Bi.
In a reaction like this one, the electron flies off at high speed (typically close to the speed of light), and the escaping electrons are the things that make large amounts of this type of radioactivity dangerous. The outgoing electron was the first thing that tipped off scientists in the early 1900s to the existence of this type of radioactivity. Since they didn't know that the outgoing particles were electrons, they called them beta particles, and this type of radioactive decay was therefore known as beta decay. A clearer but less common terminology is to call the two processes electron decay and positron decay.
The neutrino or antineutrino emitted in such a reaction pretty much ignores all matter, because its lack of charge makes it immune to electrical forces, and it also remains aloof from strong nuclear interactions. Even if it happens to fly off going straight down, it is almost certain to make it through the entire earth without interacting with any atoms in any way. It ends up flying through outer space forever. The neutrino's behavior makes it exceedingly difficult to detect, and when beta decay was first discovered nobody realized that neutrinos even existed. We now know that the neutrino carries off some of the energy produced in the reaction, but at the time it seemed that the total energy afterwards (not counting the unsuspected neutrino's energy) was greater than the total energy before the reaction, violating conservation of energy. Physicists were getting ready to throw conservation of energy out the window as a basic law of physics when indirect evidence led them to the conclusion that neutrinos existed.
Discussion Questions
A In the reactions n->p+e^-+barnu and p->n+e^++nu, verify that charge is conserved. In beta decay, when one of these reactions happens to a neutron or proton within a nucleus, one or more gamma rays may also be emitted. Does this affect conservation of charge? Would it be possible for some extra electrons to be released without violating charge conservation?
B When an antielectron and an electron annihilate each other, they produce two gamma rays. Is charge conserved in this reaction?
Fusion
As we have seen, heavy nuclei tend to fly apart because each proton is being repelled by every other proton in the nucleus, but is only attracted by its nearest neighbors. The nucleus splits up into two parts, and as soon as those two parts are more than about 1 fm apart, the strong nuclear force no longer causes the two fragments to attract each other. The electrical repulsion then accelerates them, causing them to gain a large amount of kinetic energy. This release of kinetic energy is what powers nuclear reactors and fission bombs.
It might seem, then, that the lightest nuclei would be the most stable, but that is not the case. Let's compare an extremely light nucleus like 4He with a somewhat heavier one, 16O. A neutron or proton in 4He can be attracted by the three others, but in 16O, it might have five or six neighbors attracting it. The 16O nucleus is therefore more stable.
It turns out that the most stable nuclei of all are those around nickel and iron, having about 30 protons and 30 neutrons. Just as a nucleus that is too heavy to be stable can release energy by splitting apart into pieces that are closer to the most stable size, light nuclei can release energy if you stick them together to make bigger nuclei that are closer to the most stable size. Fusing one nucleus with another is called nuclear fusion. Nuclear fusion is what powers our sun and other stars.

Nuclear energy and binding energies
In the same way that chemical reactions can be classified as exothermic (releasing energy) or endothermic (requiring energy to react), so nuclear reactions may either release or use up energy. The energies involved in nuclear reactions are greater by a huge factor. Thousands of tons of coal would have to be burned to produce as much energy as would be produced in a nuclear power plant by one kg of fuel.
Although nuclear reactions that use up energy (endothermic reactions) can be initiated in accelerators, where one nucleus is rammed into another at high speed, they do not occur in nature, not even in the sun. The amount of kinetic energy required is simply not available.
To find the amount of energy consumed or released in a nuclear reaction, you need to know how much nuclear interaction energy, U_(\n\uc), was stored or released. Experimentalists have determined the amount of nuclear energy stored in the nucleus of every stable element, as well as many unstable elements. This is the amount of mechanical work that would be required to pull the nucleus apart into its individual neutrons and protons, and is known as the nuclear binding energy.
Example 6: A reaction occurring in the sun
The sun produces its energy through a series of nuclear fusion reactions. One of the reactions is
1H+2H->3He+gamma
The excess energy is almost all carried off by the gamma ray (not by the kinetic energy of the helium-3 atom). The binding energies in units of pJ (picojoules) are:
| 1H | 0 J |
| 2H | 0.35593 pJ |
| 3He | 1.23489 pJ |
The total initial nuclear energy is 0 pJ+0.35593 pJ, and the final nuclear energy is 1.23489 pJ, so by conservation of energy, the gamma ray must carry off 0.87896 pJ of energy. The gamma ray is then absorbed by the sun and converted to heat.
self-check C
Why is the binding energy of 1H exactly equal to zero?
Figure ac is a compact way of showing the vast variety of the nuclei. Each box represents a particular number of neutrons and protons. The black boxes are nuclei that are stable, i.e., that would require an input of energy in order to change into another. The gray boxes show all the unstable nuclei that have been studied experimentally. Some of these last for billions of years on the average before decaying and are found in nature, but most have much shorter average lifetimes, and can only be created and studied in the laboratory.

The curve along which the stable nuclei lie is called the line of stability. Nuclei along this line have the most stable proportion of neutrons to protons. For light nuclei the most stable mixture is about 50-50, but we can see that stable heavy nuclei have two or three times more neutrons than protons. This is because the electrical repulsions of all the protons in a heavy nucleus add up to a powerful force that would tend to tear it apart. The presence of a large number of neutrons increases the distances among the pro- tons, and also increases the number of attractions due to the strong nuclear force.
Biological effects of ionizing radiation
Units used to measure exposure
 As a science educator, I find it frustrating that nowhere in the massive amount of journalism devoted to nuclear safety does one ever find any numerical statements about the amount of radiation to which people have been exposed. Anyone capable of understanding sports statistics or weather reports ought to be able to understand such measurements, as long as something like the following explanatory text was inserted somewhere in the article:
As a science educator, I find it frustrating that nowhere in the massive amount of journalism devoted to nuclear safety does one ever find any numerical statements about the amount of radiation to which people have been exposed. Anyone capable of understanding sports statistics or weather reports ought to be able to understand such measurements, as long as something like the following explanatory text was inserted somewhere in the article:
Radiation exposure is measured in units of Sieverts (Sv). The average person is exposed to about 2000 μSv (microSieverts) each year from natural background sources.
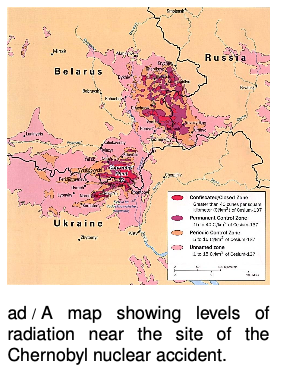
With this context, people would be able to come to informed conclusions. For example, figure ad shows a scary-looking map of the levels of radiation in the area surrounding the 1986 nuclear accident at Chernobyl, Ukraine, the most serious that has ever occurred. At the boundary of the most highly contaminated (bright red) areas, people would be exposed to about 13,000 μSv per year, or about four times the natural background level. In the pink areas, which are still densely populated, the exposure is comparable to the natural level found in a high-altitude city such as Denver.
 What is a Sievert? It measures the amount of energy per kilogram deposited in the body by ionizing radiation, multiplied by a “quality factor” to account for the different health hazards posed by alphas, betas, gammas, neutrons, and other types of radiation. Only ionizing radiation is counted, since nonionizing radiation simply heats one’s body rather than killing cells or altering DNA. For instance, alpha particles are typically moving so fast that their kinetic energy is sufficient to ionize thousands of atoms, but it is possible for an alpha particle to be moving so slowly that it would not have enough kinetic energy to ionize even one atom.
What is a Sievert? It measures the amount of energy per kilogram deposited in the body by ionizing radiation, multiplied by a “quality factor” to account for the different health hazards posed by alphas, betas, gammas, neutrons, and other types of radiation. Only ionizing radiation is counted, since nonionizing radiation simply heats one’s body rather than killing cells or altering DNA. For instance, alpha particles are typically moving so fast that their kinetic energy is sufficient to ionize thousands of atoms, but it is possible for an alpha particle to be moving so slowly that it would not have enough kinetic energy to ionize even one atom.
Unfortunately, most people don’t know much about radiation and tend to react to it based on unscientific cultural notions. These may, as in figure ae, be based on fictional tropes silly enough to require the suspension of disbelief by the audience, but they can also be more subtle. People of my kids’ generation are more familiar with the 2011 Fukushima nuclear accident that with the much more serious Chernobyl accident. The news coverage of Fukushima showed scary scenes of devastated landscapes and distraught evacuees, implying that people had been killed and displaced by the release of radiation from the reaction. In fact, there were no deaths at all due to the radiation released at Fukushima, and no excess cancer deaths are statistically predicted in the future. The devastation and the death toll of 16,000 were caused by the earthquake and tsunami, which were also what damaged the plant.
Effects of exposure
Notwithstanding the pop culture images like figure af, it is not possible for a multicellular animal to become “mutated” as a whole. In most cases, a particle of ionizing radiation will not even hit the DNA, and even if it does, it will only affect the DNA of a single cell, not every cell in the animal’s body. Typically, that cell is simply killed, because the DNA becomes unable to function properly. Once in a while, however, the DNA may be altered so as to make that cell cancerous. For instance, skin cancer can be caused by UV light hitting a single skin cell in the body of a sunbather. If that cell becomes cancerous and begins reproducing uncontrollably, she will end up with a tumor twenty years later.
Other than cancer, the only other dramatic effect that can result from altering a single cell’s DNA is if that cell happens to be a sperm or ovum, which can result in nonviable or mutated offspring. Men are relatively immune to reproductive harm from radiation, because their sperm cells are replaced frequently. Women are more vulnerable because they keep the same set of ova as long as they live.
Effects of high doses of radiation
A whole-body exposure of 5,000,000 μSv will kill a person within a week or so. Luckily, only a small number of humans have ever been exposed to such levels: one scientist working on the Manhattan Project, some victims of the Nagasaki and Hiroshima explosions, and 31 workers at Chernobyl. Death occurs by massive killing of cells, especially in the blood-producing cells of the bone marrow.
Effects of low doses of radiation
 Lower levels, on the order of 1,000,000 μSv, were inflicted on some people at Nagasaki and Hiroshima. No acute symptoms result from this level of exposure, but certain types of cancer are significantly more common among these people. It was originally expected that the radiation would cause many mutations resulting in birth defects, but very few such inherited effects have been observed.
Lower levels, on the order of 1,000,000 μSv, were inflicted on some people at Nagasaki and Hiroshima. No acute symptoms result from this level of exposure, but certain types of cancer are significantly more common among these people. It was originally expected that the radiation would cause many mutations resulting in birth defects, but very few such inherited effects have been observed.
A great deal of time has been spent debating the effects of very low levels of ionizing radiation. The following table gives some sample figures.
| maximum beneficial does per day | ~ 10,000 muSv |
| CT scan | ~ 10,000 muSv |
| natural background per year | 2,000-7,000 muSv |
| health guidelines for exposure to a fetus | 1,000 muSv |
| flying from New York to Tokyo | 150 muSv |
| chest x-ray | 50 muSv |
Note that the largest number, on the first line of the table, is the maximum beneficial dose. The most useful evidence comes from experiments in animals, which can intentionally be exposed to significant and well measured doses of radiation under controlled conditions. Experiments show that low levels of radiation activate cellular damage control mechanisms, increasing the health of the organism. For example, exposure to radiation up to a certain level makes mice grow faster; makes guinea pigs’ immune systems function better against diptheria; increases fertility in trout and mice; improves fetal mice’s resistance to disease; increases the life-spans of flour beetles and mice; and reduces mortality from cancer in mice. This type of effect is called radiation hormesis.
There is also some evidence that in humans, small doses of radiation increase fertility, reduce genetic abnormalities, and reduce mortality from cancer. The human data, however, tend to be very poor compared to the animal data. Due to ethical issues, one cannot do controlled experiments in humans. For example, one of the best sources of information has been from the survivors of the Hiroshima and Nagasaki bomb blasts, but these people were also exposed to high levels of carcinogenic chemicals in the smoke from their burning cities; for comparison, firefighters have a heightened risk of cancer, and there are also significant concerns about cancer from the 9/11 attacks in New York. The direct empirical evidence about radiation hormesis in humans is therefore not good enough to tell us anything unambiguous,3 and the most scientifically reasonable approach is to assume that the results in animals also hold for humans: small doses of radiation in humans are beneficial, rather than harmful. However, a variety of cultural and historical factors have led to a situation in which public health policy is based on the assumption, known as “linear no-threshold” (LNT), that even tiny doses of radiation are harmful, and that the risk they carry is proportional to the dose. In other words, law and policy are made based on the assumption that the effects of radiation on humans are dramatically different than its effects on mice and guinea pigs. Even with the unrealistic assumption of LNT, one can still evaluate risks by comparing with natural background radiation. For example, we can see that the effect of a chest x-ray is about a hundred times smaller than the effect of spending a year in Colorado, where the level of natural background radiation from cosmic rays is higher than average, due to the high altitude. Dropping the implausible LNT assumption, we can see that the impact on one’s health of spending a year in Colorado is likely to be positive, because the excess radiation is below the maximum beneficial level.
The green case for nuclear power
In the late twentieth century, antinuclear activists largely succeeded in bringing construction of new nuclear power plants to a halt in the U.S. Ironically, we now know that the burning of fossil fuels, which leads to global warming, is a far more grave threat to the environment than even the Chernobyl disaster. A team of biologists writes: “During recent visits to Chernobyl, we experienced numerous sightings of moose (Alces alces), roe deer (Capreol capreolus), Russian wild boar (Sus scrofa), foxes (Vulpes vulpes), river otter (Lutra canadensis), and rabbits (Lepus europaeus) ... Diversity of flowers and other plants in the highly radioactive regions is impressive and equals that observed in protected habitats outside the zone
 ... The observation that typical human activity (industrialization, farming, cattle raising, collection of firewood, hunting, etc.) is more devastating to biodiversity and abundance of local flora and fauna than is the worst nuclear power plant disaster validates the negative impact the exponential growth of human populations has on wildlife.”4
... The observation that typical human activity (industrialization, farming, cattle raising, collection of firewood, hunting, etc.) is more devastating to biodiversity and abundance of local flora and fauna than is the worst nuclear power plant disaster validates the negative impact the exponential growth of human populations has on wildlife.”4
Nuclear power is the only source of energy that is sufficient to re- place any significant percentage of energy from fossil fuels on the rapid schedule demanded by the speed at which global warming is progressing. People worried about the downside of nuclear energy might be better off putting their energy into issues related to nu- clear weapons: the poor stewardship of the former Soviet Union’s warheads; nuclear proliferation in unstable states such as Pakistan; and the poor safety and environmental history of the superpowers’ nuclear weapons programs, including the loss of several warheads in plane crashes, and the environmental disaster at the Hanford, Washington, weapons plant.
Protection from radiation
People do sometimes work with strong enough radioactivity that there is a serious health risk. Typically the scariest sources are those used in cancer treatment and in medical and biological research. Also, a dental technician, for example, needs to take precautions to avoid accumulating a large radiation dose from giving dental x-rays to many patients. There are three general ways to reduce exposure: time, distance, and shielding. This is why a dental technician doing x-rays wears a lead apron (shielding) and steps outside of the x-ray room while running an exposure (distance). Reducing the time of exposure dictates, for example, that a person working with a hot cancer-therapy source would minimize the amount of time spent near it.
Shielding against alpha and beta particles is trivial to accomplish. (Alphas can’t even penetrate the skin.) Gammas and x-rays interact most strongly with materials that are dense and have high atomic numbers, which is why lead is so commonly used. But other mate- rials will also work. For example, the reason that bones show up so clearly on x-ray images is that they are dense and contain plenty of calcium, which has a higher atomic number than the elements found in most other body tissues, which are mostly made of water.
 Neutrons are difficult to shield against. Because they are electrically neutral, they don’t interact intensely with matter in the same way as alphas and betas. They only interact if they happen to collide head-on with a nucleus, and that doesn’t happen very often because nuclei are tiny targets. Kinematically, a collision can transfer kinetic energy most efficiently when the target is as low in mass as possible compared to the projectile. For this reason, substances that contain a lot of hydrogen make the best shielding against neutrons. Blocks of paraffin wax from the supermarket are often used for this purpose.
Neutrons are difficult to shield against. Because they are electrically neutral, they don’t interact intensely with matter in the same way as alphas and betas. They only interact if they happen to collide head-on with a nucleus, and that doesn’t happen very often because nuclei are tiny targets. Kinematically, a collision can transfer kinetic energy most efficiently when the target is as low in mass as possible compared to the projectile. For this reason, substances that contain a lot of hydrogen make the best shielding against neutrons. Blocks of paraffin wax from the supermarket are often used for this purpose.
* The creation of the elements
Creation of hydrogen and helium in the Big Bang
Did all the chemical elements we’re made of come into being in the big bang?5 Temperatures in the first microseconds after the big bang were so high that atoms and nuclei could not hold together at all. After things had cooled down enough for nuclei and atoms to exist, there was a period of about three minutes during which the temperature and density were high enough for fusion to occur, but not so high that atoms could hold together. We have a good, detailed understanding of the laws of physics that apply under these conditions, so theorists are able to say with confidence that the only element heavier than hydrogen that was created in significant quantities was helium.
We are stardust
In that case, where did all the other elements come from? Astronomers came up with the answer. By studying the combinations of wavelengths of light, called spectra, emitted by various stars, they had been able to determine what kinds of atoms they contained. (We will have more to say about spectra at the end of this book.) They found that the stars fell into two groups. One type was nearly 100% hydrogen and helium, while the other contained 99% hydrogen and helium and 1% other elements. They interpreted these as two generations of stars. The first generation had formed out of clouds of gas that came fresh from the big bang, and their composition reflected that of the early universe. The nuclear fusion reactions by which they shine have mainly just increased the proportion of helium relative to hydrogen, without making any heavier elements. The members of the first generation that we see today, however, are only those that lived a long time. Small stars are more miserly with their fuel than large stars, which have short lives. The large stars of the first generation have already finished their lives. Near the end of its lifetime, a star runs out of hydrogen fuel and undergoes a series of violent and spectacular reorganizations as it fuses heavier and heavier elements. Very large stars finish this sequence of events by undergoing supernova explosions, in which some of their material is flung off into the void while the rest collapses into an exotic object such as a black hole or neutron star.
The second generation of stars, of which our own sun is an example, condensed out of clouds of gas that had been enriched in heavy elements due to supernova explosions. It is those heavy elements that make up our planet and our bodies.
Discussion questions
A Should the quality factor for neutrinos be very small, because they mostly don’t interact with your body?
B Would an alpha source be likely to cause different types of cancer depending on whether the source was external to the body or swallowed in contaminated food? What about a gamma source?
Calculators and Collections
- Comments
- Attachments
- Stats
No comments |
