22.1 The stage and the actors by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license. 

22.1 The stage and the actors

The Newtonian picture has particles interacting with each other by exerting forces from a distance, and these forces are imagined to occur without any time delay. For example, suppose that super-powerful aliens, angered when they hear disco music in our AM radio transmissions, come to our solar system on a mission to cleanse the universe of our aesthetic contamination. They apply a force to our sun, causing it to go flying out of the solar system at a gazillion miles an hour. According to Newton's laws, the gravitational force of the sun on the earth will immediately start dropping off. This will be detectable on earth, and since sunlight takes eight minutes to get from the sun to the earth, the change in gravitational force will, according to Newton, be the first way in which earthlings learn the bad news --- the sun will not visibly start receding until a little later. Although this scenario is fanciful enough to be at home in the pages of Cosmic Stories, it shows a real feature of Newton's laws: that information can be transmitted from one place in the universe to another with zero time delay, so that transmission and reception occur at exactly the same instant.

Newton was sharp enough to realize that this required a nontrivial assumption, which was that there was some completely objective and well-defined way of saying whether two things happened at exactly the same instant. He stated this assumption explicitly: “Absolute, true, and mathematical time, of itself, and from its own nature flows at a constant rate without regard to anything external...”

No absolute time

Ever since Einstein, we've known that this assumption was false. When Einstein first began to develop the theory of relativity, around 1905, the only real-world observations he could draw on were ambiguous and indirect. Today, the evidence is part of everyday life. For example, every time you use a GPS receiver, figure a, you're using Einstein's theory of relativity. Somewhere between 1905 and today, technology became good enough to allow conceptually simple experiments that students in the early 20th century could only discuss in terms like “Imagine that we could...” A good jumping-on point is 1971. In that year, J.C. Hafele and R.E. Keating brought atomic clocks aboard commercial airliners, b, and flew around the world, once from east to west and once from west to east. Hafele and Keating observed that there was a discrepancy between the times measured by the traveling clocks and the times measured by similar clocks that stayed home at the U.S. Naval Observatory in Washington. The east-going clock lost time, ending up off by `?59±10` nanoseconds, while the west-going one gained `273±7 ns`. Although this example is particularly dramatic, a large number of other experiments have also confirmed that time is not absolute, as Newton had imagined.

Nevertheless, the effects that Hafele and Keating observed were small. This makes sense: Newton's laws have already been thoroughly tested by experiments under a wide variety of conditions, so a new theory like relativity must agree with Newton's to a good approximation, within the Newtonian theory's realm of applicability. This requirement of backward-compatibility is known as the correspondence principle.

Causality

It's also reassuring that the effects on time were small compared to the three-day lengths of the plane trips. There was therefore no opportunity for paradoxical scenarios such as one in which the east-going experimenter arrived back in Washington before he left and then convinced himself not to take the trip. A theory that maintains this kind of orderly relationship between cause and effect is said to satisfy causality.

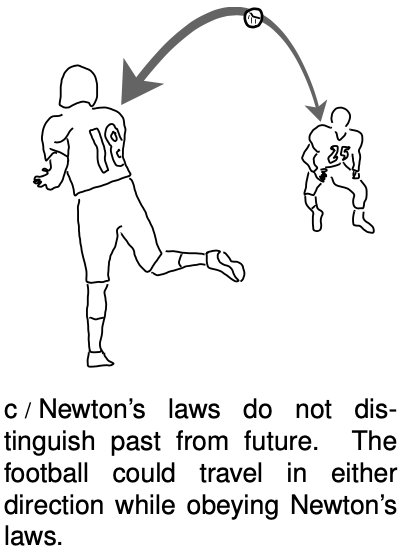
Causality is like a water-hungry front-yard lawn in Los Angeles: we know we want it, but it's not easy to explain why. Even in plain old Newtonian physics, there is no clear distinction between past and future. In figure c, number 18 throws the football to number 25, and the ball obeys Newton's laws of motion. If we took a video of the pass and played it backward, we would see the ball flying from 25 to 18, and Newton's laws would still be satisfied. Nevertheless, we have a strong psychological impression that there is a forward arrow of time. I can remember what the stock market did last year, but I can't remember what it will do next year. Joan of Arc's military victories against England caused the English to burn her at the stake; it's hard to accept that Newton's laws provide an equally good description of a process in which her execution in 1431 caused her to win a battle in 1429. There is no consensus at this point among physicists on the origin and significance of time's arrow, and for our present purposes we don't need to solve this mystery. Instead, we merely note the empirical fact that, regardless of what causality really means and where it really comes from, its behavior is consistent. Specifically, experiments show that if an observer in a certain frame of reference observes that event A causes event B, then observers in other frames agree that A causes B, not the other way around. This is merely a generalization about a large body of experimental results, not a logically necessary assumption. If Keating had gone around the world and arrived back in Washington before he left, it would have disproved this statement about causality.

Time delays in forces exerted at a distance

Relativity is closely related to electricity and magnetism, and we will go into relativity in more detail in chapters 24-27. What we care about for now is that relativity forbids Newton's instantaneous action at a distance. For suppose that instantaneous action at a distance existed. It would then be possible to send signals from one place in the universe to another without any time lag. This would allow perfect synchronization of all clocks. But the Hafele-Keating experiment demonstrates that clocks A and B that have been initially synchronized will drift out of sync if one is in motion relative to the other. With instantaneous transmission of signals, we could determine, without having to wait for A and B to be reunited, which was ahead and which was behind. Since they don't need to be reunited, neither one needs to undergo any acceleration; each clock can fix an inertial frame of reference, with a velocity vector that changes neither its direction nor its magnitude. But this violates the principle that constant-velocity motion is relative, because each clock can be considered to be at rest, in its own frame of reference. Since no experiment has ever detected any violation of the relativity of motion, we conclude that instantaneous action at a distance is impossible.

Since forces can't be transmitted instantaneously, it becomes natural to imagine force-effects spreading outward from their source like ripples on a pond, and we then have no choice but to impute some physical reality to these ripples. We call them fields, and they have their own independent existence. Chapters 22-24 are mainly about the electric and magnetic fields, although we'll also talk about the gravitational field. Ripples of the electric and magnetic fields turn out to be light waves. Fields don't have to wiggle; they can hold still as well. The earth's magnetic field, for example, is nearly constant, which is why we can use it for direction-finding.

Even empty space, then, is not perfectly featureless. It has measurable properties. For example, we can drop a rock in order to measure the direction of the gravitational field, or use a magnetic compass to find the direction of the magnetic field. This concept made a deep impression on Einstein as a child. He recalled that as a five-year-old, the gift of a magnetic compass convinced him that there was “something behind things, something deeply hidden.”

More evidence that fields of force are real: they carry energy.

The smoking-gun argument for this strange notion of traveling force ripples comes from the fact that they carry energy. In figure d/1, Alice and Betty hold positive charges A and B at some distance from one another. If Alice chooses to move her charge closer to Betty's, d/2, Alice will have to do some mechanical work against the electrical repulsion, burning off some of the calories from that chocolate cheesecake she had at lunch. This reduction in her body's chemical energy is offset by a corresponding increase in the electrical potential energy `qDeltaV`. Not only that, but 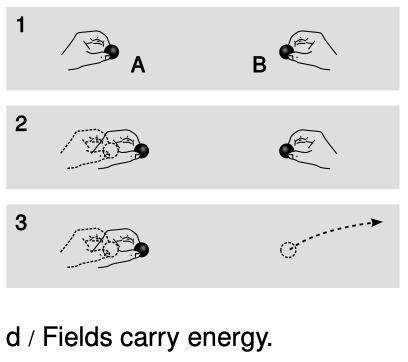Alice feels the resistance stiffen as the charges get closer together and the repulsion strengthens. She has to do a little extra work, but this is all properly accounted for in the electrical potential energy.

But now suppose, d/3, that Betty decides to play a trick on Alice by tossing charge B far away just as Alice is getting ready to move charge A. We have already established that Alice can't feel charge B's motion instantaneously, so the electric forces must actually be propagated by an electric field. Of course this experiment is utterly impractical, but suppose for the sake of argument that the time it takes the change in the electric field to propagate across the diagram is long enough so that Alice can complete her motion before she feels the effect of B's disappearance. She is still getting stale information about B's position. As she moves A to the right, she feels a repulsion, because the field in her region of space is still the field caused by B in its old position. She has burned some chocolate cheesecake calories, and it appears that conservation of energy has been violated, because these calories can't be properly accounted for by any interaction with B, which is long gone.

If we hope to preserve the law of conservation of energy, then the only possible conclusion is that the electric field itself carries away the cheesecake energy. In fact, this example represents an impractical method of transmitting radio waves. Alice does work on charge A, and that energy goes into the radio waves. Even if B had never existed, the radio waves would still have carried energy, and Alice would still have had to do work in order to create them.

Discussion Questions

A   Amy and Bill are flying on spaceships in opposite directions at such high velocities that the relativistic effect on time's rate of flow is easily noticeable. Motion is relative, so Amy considers herself to be at rest and Bill to be in motion. She says that time is flowing normally for her, but Bill is slow. But Bill can say exactly the same thing. How can they both think the other is slow? Can they settle the disagreement by getting on the radio and seeing whose voice is normal and whose sounds slowed down and Darth-Vadery?

22.1 The stage and the actors by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.